LBM开篇

LBM流体计算

LBM的发展

20世纪50年代初，现代计算机之父冯$ \cdot $ 诺依曼(vonNeuman)为模拟生物发育中细胞的自我复制提出了元胞自动机的雏形。随后1970年，剑桥大学的J.H.Conway设计了一种计算机游戏—$``$生命的游戏$”$ 。它是具有产生动态图案和动态结构能力的元胞自动机模型，吸引了众多科学家的兴趣，推动了元胞自动机研究的迅速发展。之后，S.Wolfram对初等元胞自动机的256种规则产生的所有模型进行了详细而深入的研究。他还用熵来描述其演化行为，把元胞自动机分为：平稳型、周期型、混沌型、复杂型四类。近年来随着复杂性研究的进展，作为探索复杂系统的一种有效工具，元胞自动机获得了深入的研究和广泛的应用。

1986年，法国科学计算中心Frisch，Hasslacher和Pomeau¹提供了第一个能够恢复Navier-Stokes方程的晶格气自动机。 他们表明，当碰撞规则保留质量和动量时，如果下面的晶格具有足够的对称性（至少在二维上是六边形的），则晶格气体自动机可以在宏观统计中推导得到Navier-Stokes方程。

为了解决格子Boltzmann自动机的高统计噪声问题，McNamara和Zanetti²于1988年首次提出了一个新模型：Lattice Boltzmann方程。 基本思想十分简单：用浮点变量（对应于分子的分布函数）替换细胞自动机的布尔变量（对应于单个布尔分子）。 随后1989年，Higuera等³人使用线化形式的碰撞算子增加了高雷诺数条件下的流场稳定性。

无论是在理论、应用还是性能上，LBM都取得了非常重大的进步和发展。相比传统的CFD方法直接离散并求解流体力学的宏观方程，而LB法则求解离散的动力学方程，并在宏观范围内再现流体力学方程。 主要包含流（stream）和碰撞（collision）两个步骤：流步骤是线性且精确的，所有非线性都在碰撞步骤中局部建模。 相反，NS方程中的对流项是非线性且非局部的。 压力场通过局部LB方法获得的，从而避免了像传统方法那样需要耗时的椭圆泊松方程求解的需要。流步骤的精确对流与改进的松弛算法（MRT）的碰撞步骤相结合，使其具有较低数值耗散的二阶精确方法。也可以调整碰撞步骤的动力学模型，以根据需要引入其他物理原理，并且可以调整其附加自由度以提高数值稳定性。同时，LBM更易于实现且高效并行，同时具有足够的通用性。近年来，GPU图形处理单元作为通用计算平台的兴起，也为LBM的并行化高速计算开辟了新的道路。

在过去的25年中，无数科学爱好者提出了许多模型^4,5，以提高LBM的精度和数值稳定性，并成功应用于许多领域，例如多孔介质⁶中的流，湍流⁷，多相流⁸，热驱动流⁹，可压缩流¹⁰，电子流动¹¹等等。 尽管起初很多人抱着怀疑的心态看待（并且至今仍在怀疑），但现在不可否认LBM已被科学界接受为模拟流体流动的可行方法。在商业领域， Ultrafluidx 、powerflow、Xflow、palabos等软件的不断兴起也证明了LBM的实用性。其数值稳定性，物理精度，对多个问题的适应性以及在多核体系结构上的数值效率使其成为下一代流体流动求解器的理想选择。

LBM的理论基础

宏观与介观

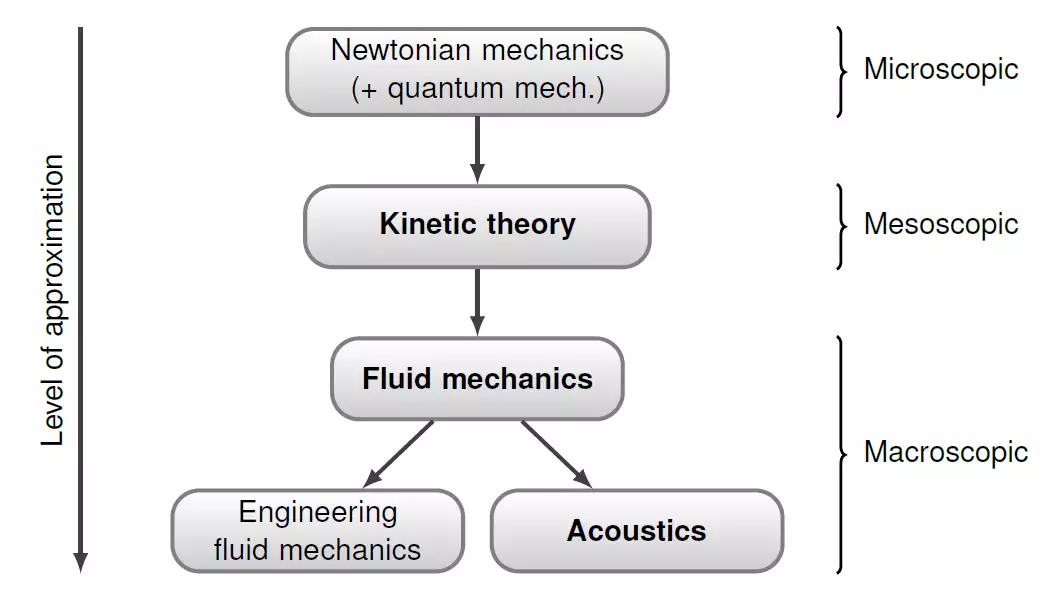
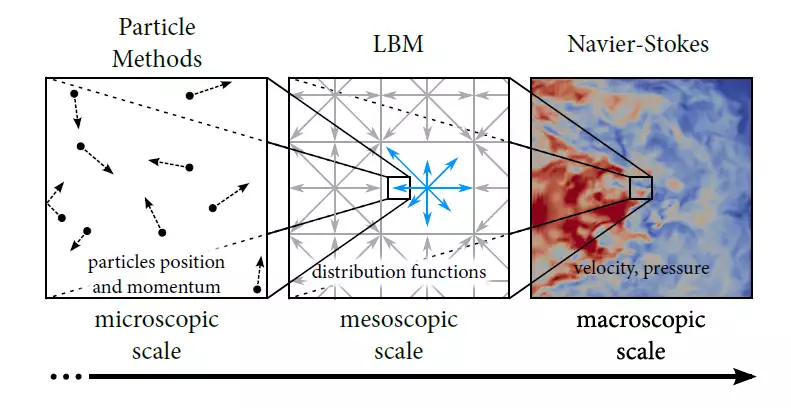
• 微观尺度：分子尺度。 在此尺度下，粒子具有弹道轨迹（布朗运动），其平均微观速度由温度给出。这是分子动力学和光滑粒子流体动力学试图在某种程度上复制的尺度。

• 介观尺度：粒子平均统计量。通过动力学理论研究了粒子分布函数的演变。分布函数存在于相空间中，分布函数表示每单位体积的粒子数，该单位体积在周围的体积内具有速度、位置和时间。LBM正是采用这种观点。

• 宏观尺度：矢量场（例如流体速度）和标量场（例如压力或温度）变化的尺度。与微观和介观尺度相比，该尺度足够大，可以将流体视为连续体，因此在每个位置和每个时间可定义这些宏观量。例如，速度可以写成，压力写成。这些宏观量的行为可以通过Navier-Stokes方程准确地描述。

动力学理论是统计力学的一个分支，涉及非平衡过程的动力学及其对热力学平衡的松弛。该理论基于物质的分子假设，假设物质不是连续的，而是由大量（但有限）的称为分子的小物体组成。通过考虑组成分子的微观运动来解释气体的宏观特性，例如压力，温度，粘度，热导率等。气体演化的宏观定律可以通过动力学理论的分子描述来预测，并预测热力学的第二定律，这是自然界最基本的定律之一，它表明密闭系统的熵总是增加（熵增定律）。

Bolzmann方程

玻尔兹曼方程是动力学理论的基石，它由奥地利物理学家路德维希$ \cdot $ 爱德华$ \cdot $ 玻尔兹曼（Ludwig Eduard Boltzmann，1844-1906年）提出。其最大的成就是在统计力学的发展中，解释并预测了原子的性质及其如何决定物质的宏观性质。

该方程用微观动力学相互作用描述了分布函数 $f ( x, \xi ,t ) $ 的演化。尽管这个方程建立于一个多世纪以前，但直到2011年才获得了关于整体存在和经典解快速衰减到平衡的形式化数学证明¹³。

玻尔兹曼方程可写为：

$$\begin{equation} \frac{ \partial f}{ \partial t}+ \xi ⋅\triangledown f+\frac{F}{ \rho }⋅\triangledown _{ \xi }f= \Omega \left( f \right) \end{equation}$$

​

其中， $ \triangledown _{ \xi }f $ 是分布函数在速度空间的梯度， $ \Omega $ 为碰撞算子。

碰撞算子可以根据实际物理条件，有不同的定义方式。但至少必须得满足三个守恒定理：

• 质量守恒：$ \int \Omega \left( f \right) d \xi =0 $
• 动量守恒：$ \int \xi \Omega \left( f \right) d \xi =0 $
• 能量守恒: $ \int \vert \xi \vert ^{2} \Omega \left( f \right) d \xi =0 \space or \int \vert \xi \vert ^{2} \Omega \left( f \right) d \xi =0 $

其中，因为 $ \vert v \vert ^{2}= \vert \xi -u \vert = \vert \xi \vert ^{2}-2 \xi ⋅u+ \vert u \vert ^{2} $ 并结合质量和动量守恒，可推导得到两个能量形式等价。

宏观参数通过对 $ f $ 求矩获得：

$$\Pi _{0}= \int fd \xi = \rho$$ $$\Pi_{\alpha}=\int \xi _{ \alpha } fd \xi = \rho u _ {\alpha}$$ $$\Pi _{ \alpha \beta }= \int \xi _{ \alpha } \xi _{ \beta }fd \xi$$ $$\Pi _{ \alpha \beta \gamma }= \int \xi _{ \alpha } \xi _{ \beta } \xi _{ \gamma }fd \xi$$

如果有需要，可以进一步求解高阶矩。

Maxwell-Boltzmann 平衡态

当两个粒子碰撞时，它们的速度会改变。新速度取决于碰撞前的位置和速度以及碰撞过程中的分子间作用力。 但是，我们可以假设碰撞倾向于使粒子的速度围绕其平均速度u在所有方向上的均匀分布。这意味着，如果我们采用具有任何初始分布的粒子气体并将其放置足够长的时间，它将最终达到一个平衡状态，在该状态下，额外速度v的所有方向都可能相等。

速度的这种均匀分布意味着分布函数 $ f^{0} $仅取决于额外速度v在三维笛卡尔坐标系中, $ \vert v \vert ^{2}= \vert v{x}^{2}+v{y}^{2}+v{z}^{2} \vert $，三个方向是为相等，并假设 $ f^{0} \left( \vert v \vert \right) =f{x}^{0} \left( v{x} \right) f{y}^{0} \left( v{y} \right) f{z}^{0} \left( v_{z} \right) $。

对于恒定 $ \vert v \vert ^{2} $ 来说， $ f^{0} \left( \vert v \vert \right) $ 也是相对恒定的，因此，

$$\begin{eqnarray} \ln f_{x}^{0} \left( v_{x} \right) +lnf_{y}^{0} \left( v_{y} \right) +lnf_{z}^{0} \left( v_{z} \right) =const.\ \\ \end{eqnarray}$$

假定方程可解，则有如下待定系数形式：

$$\ln f_{x}^{0} \left( v_{x} \right) =a-bv_{x}^{2} \Rightarrow f_{x}^{0} \left( v_{x} \right) =e^{a}e^{-bv_{x}^{2}}\ \\$$

那么，平衡状态下的分布函数有以下形式：

$$\ln f_{x}^{0} \left( v \right) =e^{3a}e^{-b \left( v_{x}^{2}+v_{y}^{2}+v_{z}^{2} \right) }=e^{3a}e^{-bv_{x}^{2}}\ \\$$

参数a和b可以通过对 $ f^{0} $ 求0阶矩（密度）和二阶矩（能量）求得：

$$\rho = \int f^{0} \left( \vert v \vert \right) d \xi \ \\ \rho e= \int _{-\infty}^{+\infty} \vert v \vert ^{2}f^{0} \left( v \right) d \xi \ \\$$

最终，得到满足条件的一种平衡分布函数形式：

$$f^{0} \left( \rho ,u,T, \xi \right) =f^{0} \left( \vert v \vert \right) =\frac{ \rho }{ \left( 2 \pi RT \right) ^{\frac{3}{2}}}e^{-\frac{ \vert \xi -u \vert ^{2}}{2RT}}\ \\$$

该分布特性与温度有关，该平衡分布称为Maxwell-Boltzmann分布。它最初是由James Clerk Maxwell使用与我们在此处使用的推导相似的推导发现的，后来由Ludwig Boltzmann使用更严格的统计机制得到。

BGK model（单弛豫时间（SRT））

玻尔兹曼最初的碰撞算子是速度空间上复杂的双积分形式。对于粒子之间的分子间力的任何选择，它基本上考虑了所有可能的两个粒子碰撞的结果。该碰撞算子满足守恒条件，但是求解非常麻烦。后来提出了一些替代碰撞模型，其目的是要找到一种碰撞模型，该模型比Boltzmann的原始模型简单，但仍能提供大致正确的宏观行为。

BGK碰撞算子模型是广为熟知的一种：

$$\Omega \left( f \right) =-\frac{1}{ \tau} \left( f-f^{0} \right) \ \\$$

其中， $ \tau $ 称为弛豫时间，表明气体向平衡算子松弛的速度有多快。这是由Bhatnagar，Gross和Krook[25]在1954年提出的，它是一种非常简单的粒子碰撞模型。

BGK算子通过直接对松弛过程建模而不是尝试遵循碰撞的细节来捕获此行为。

由于平衡分布 $ f^{0} $ 具有与分布函数 $ f $ 相同的密度，动量和能量矩，可以很容易地证明BGK算子满足质量，动量和能量守恒。

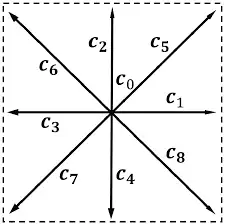
这里通过二维D2Q9格子举例。离散速度分量 $ e_{ \alpha } $ 如图，具有如下形式：

$$f(n) = \begin{cases} \left( \text{0, 0} \right) , & \alpha =0 \\\\ \left( \pm 1,0 \right) , \left( 0, \pm 1 \right), & \alpha =1, \ldots ,4 \\\\ \left( \pm 1, \pm 1 \right), & \alpha =5, \ldots ,8 \end{cases}$$

最终，其离散Boltzmann演化方程可以写成：

$$f_{ \alpha } \left( x+e_{ \alpha },t+1 \right) =f_{ \alpha } \left( x,t \right) -\frac{1}{ \tau} \left[ f_{ \alpha } \left( x,t \right) -f_{ \alpha }^{0} \left( x,t \right) \right]$$

现在，让我们将Hermite级数展开应用于 $ \xi $ -space中的平衡分布函数 $ f^{0} \left( \rho ,u,T, \xi \right) $ ：

$$f^{0} \left( x, \xi ,t \right) \approx w \left( \xi \right) \sum _{n=0}^{N}\frac{1}{n!}a^{n} \left( x,t \right) ⋅H^{n} \left( \xi \right)$$

根据Hermite函数的性质,前两个展开系数满足和守恒公式类似的形式。

现在我们只截断前两阶，显式地写出的平衡分布函数多项式形式的近似解：

$$f_{ \alpha }^{0}=w_{ \alpha } \rho \left( 1+\frac{e_{ \alpha }⋅u}{c_{s}^{2}}-\frac{u⋅u}{2c_{s}^{2}} \right)$$

其中， $ w{ \alpha } $ 是不同粒子方向上的加权因子，对D2Q9格子来说， $ w{0}=4/9 $ ， $ w{ \alpha }=1/9 $ , $ ~ \alpha =1,2,3,4, w{ \alpha }=1/36 $ ， $ \alpha =5,6,7,8 $ 。 $ c{s}^{2}=1/3 $ 。可以验证，通过获取 $ f{ \alpha }^{0} $ 的零和一阶矩来更新流体动力场，即密度和速度，并通过状态方程从密度中获得压力场p：

$$\rho= \sum_{ \alpha } {f_\alpha} \\\\ \rho u= \sum_{ \alpha } {f_\alpha } {e_\alpha } \\\\ p=c_{s}^{2} \rho$$

该方法模型流体运动，其动力粘度方程可以通过弛豫时间 $ \tau $ 给出：

$$\nu =c_{s}^{2} \left( \tau-\frac{1}{2} \right)$$

可能需要注意的是，当需要模拟粘度相对较低的流体时，这种单松弛的LBM方法易于出现数值不稳定性。当 $ \tau \rightarrow 1/2 $ ，没有其他自由度可以用来增强数值稳定性。后面提出的多松弛MRT模型和中心矩模型可以有效改善该问题。

同时，也需要注意的是BGK碰撞算子只是气体中粒子碰撞结果的简化模型，不如玻尔兹曼最初的碰撞算子精确。 例如，使用BGK算子的Boltzmann方程预测Prandtl数Pr 为 1，而使用Boltzmann的Prandtl数Pr，我们得到的值Pr为2/3。Pr与粘度和导热系数碰撞算子的强度有关的无量纲数。

多弛豫时间MRT模型

d’Humières¹⁵在1992年引入了多重弛豫时间（MRT）晶格Boltzmann方程（有时称为广义LBE），以克服BGK模型的某些缺陷，并被证明是优越的。 在准确性和稳定性方面。 MRT的原理是在力矩空间而不是通常的分布函数空间中执行碰撞，这引入了新的弛豫时间（每个独立力矩一个），可以调整该弛豫时间以同时调整稳定性和准确性。

MRT模型的碰撞方程可以表示为：

$$\Omega _{MRT} \left( f \right) =M^{-1}⋅S⋅ \left( m-m^{0} \right)$$

其中 $ m $ 和 $ m^{0} $ 分别代表分布函数 $ f $ 的速度矩及其平衡矩。M是变换矩阵，该矩阵将分布函数 $ f $ 线性变换为速度矩 $ m $ ， $ m=Mf $ ， $ S $ 是对角松弛矩阵。

这里，我们通过Gram-Schmidt正交化构造 $ m^{0} $ 速度矩向量的形式为：

$$m^{0}= \left( m_{0},m_{1},m_{2},m_{3},m_{4},m_{5},m_{6},m_{7},m_{8} \right) ^{T}\\ = \left( \rho , \rho u_{x}, \rho u_{y},e,p_{xx},p_{xy},q_{x},q_{y}, \epsilon \right) ^{T}$$

这里，

$$e= \rho -3 \rho \left( u_{x}^{2}+u_{y}^{2} \right) ,p_{xx}= \rho \ast \left( u_{x}^{2}-u_{y}^{2} \right) ,\\\\ p_{xy}= \rho u_{x}u_{y},q_{x}=3 \rho u_{x}^{3}- \rho u_{x},\\\\ q_{y}=3 \rho u_{y}^{3}- \rho u_{y},~ \epsilon =9 \rho u_{x}^{2}u_{y}^{2}-3 \rho \left( u_{x}^{2}+u_{y}^{2} \right) + \rho$$

变换矩阵M:

$$M= \begin{bmatrix} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1\\\\ 0 & 1 & 0 & -1 & 0 & 1 & -1 & -1 & 1\\\\ 0 & 0 & 1 & 0 & -1 & 1 & 1 & -1 & -1\\\\ -4 & 1 & -1 & -1 & -1 & 2 & 2 & 2 & 2\\\\ 0 & 1 & -1 & 1 & -1 & 0 & 0 & 0 & 0\\\\ 0 & 0 & 0 & 0 & 0 & 1 & -1 & 1 & -1\\\\ 0 & -2 & 0 & 2 & 0 & 1 & -1 & -1 & 1\\\\ 0 & 0 & -2 & 0 & 2 & 1 & 1 & -1 & -1\\\\ 4 & -2 & -2 & -2 & -2 & 1 & 1 & 1 & 1 \\\\ \end{bmatrix}$$

对角松弛矩阵S[]:

$$S=diag \left( 0,1,1,s_{e},s_{ \nu },s_{ \nu },s_{q},s_{q},s_{ \epsilon } \right)$$

其中， $ s{ \nu }=2/\ast \left( 6 \nu +1 \right) ,s{q}=8\ast \left( 2-s{ \nu } \right) / \left( 8-s{ \nu } \right) $

除非另有说明，我们将使用 $ s{e}=s{ \nu }=s_{ \epsilon } $ ，即两次松弛时间（TRT）模型。

尽管MRT克服了BGK的一些缺陷，但它付出了相应代价：除了更高的复杂性之外，对于高阶矩的选择也不是唯一的，取决于所考虑的晶格和自由松弛的值需要针对每个问题优化速率。 此外，在静态参考系中花费一些时间并以不同的速率放松它们可能反而导致违反BGK模型中不存在的伽利略不变性问题。

Cascade LBM

现在，我们将讨论基于中心矩（central moment）的LB方案。相比前两类模型，中心矩方法将进一步提高效率和数值精度。 该方法通过将不同中心矩松弛到其对应的平衡态来表征碰撞过程。中心矩定义为所有粒子方向上分布函数乘积的总和。好处是使用中心矩自然地会对那些由给定格子独立支持的矩分量施加伽利略不变性（但对于那些由于晶格的离散性和对称性而与低阶矩混叠的高阶矩则不适用）。 这里我们介绍其中一种级联LBM（Cascade LBM）方法，采用标准的D2Q9格子说明¹⁶。

首先，我们需要构造九个非正交的基向量：

$$\Phi_{0} = { \left( 1,1,1,1,1,1,1,1,1 \right) }^T \\\\ \Phi_{1} = e_{x} = { \left( 0,1,0,-1,0,1,1,-1,-1 \right) }^T \\\\ \Phi_{2} = e_{y} = { \left( 0,0,1,0,-1,1,1,-1,-1 \right) }^T \\\\ \Phi_{3} = e_{x} ⋅ e_{x} + e_{y} ⋅ e_{y} = { \left( 0,1,1,1,1,2,2,2,2 \right) }^T \\\\ \Phi_{4} = e_{x} ⋅ e_{x} - e_{y} ⋅ e_{y} = { \left( 0,1,-1,1,-1,0,0,0,0 \right) }^T \\\\ \Phi_{5} = e_{x} ⋅ e_{y} = { \left( 0,0,0,0,0,1,-1,1,-1 \right) }^T \\\\ \Phi_{6} = e_{x} ⋅ e_{x} ⋅ e_{y} = { \left( 0,0,0,0,0,1,-1,1,-1 \right) }^T \\\\ \Phi_{7} = e_{x} ⋅ e_{y} ⋅ e_{y} = { \left( 0,0,0,0,0,1,-1,-1,1 \right) }^T \\\\ \Phi_{8} = e_{x} ⋅ e_{x} ⋅ e_{y} ⋅ e_{y} = { \left( 0,0,0,0,0,1,1,1,1 \right) }^T \\\\$$

类似MRT，通过Gram-Schmidt正交化，得到正交基向量：

$$K_{0}= \Phi_{0},K_{1}= \Phi_{1},K_{2}= \Phi_{2} \\\\ K_{3}=3 \Phi_{3} -4 \Phi_{0},K_{4}= \Phi_{4},K_{5}= \Phi_{5} \\\\ K_{6}=-3 \Phi_{6}+2 \Phi_{2},K_{7}=-3 \Phi_{7}+2 \Phi_{1},K_{8}=9 \Phi_{8}-6 \Phi_{3}+4 \Phi_{0} \\\\$$

得以构造正交矩阵 $ K= \left[ K{0},K{1},K{2},K{3},K{4},K{5},K{6},K{7},K_{8} \right] $

现在我们定义连续平衡中心矩为：

$$\Pi_{x^{m}y^{n}}^{0}= \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty}f^{0} \left( \xi_{x}-u_{x} \right) ^{m} \left( \xi_{x}-u_{y} \right)^{n}d \xi_{x}\mathrm{d} \xi_{y}$$

其离散形式为

$$k_{x^{m}y^{n}}^{0}= \sum_{ \alpha }^{}f_{ \alpha } \left( e_{ \alpha x}-u_{x} \right)^{m} \left( e_{ \alpha }-u_{y} \right)^{n}$$

同时，我们也可以将 $ k_{x^{m}y^{n}}^{‘} $ 定义f的m和\n阶混合矩。

代入Maxwell平衡分布，以及守恒公式，可以获得：

$$k_{0}^{0}= \rho ,k_{x}^{0}=0,k_{y}^{0}=0，k_{xx}^{0}=c_{s}^{2} \rho ,k_{yy}^{0}=c_{s}^{2} \rho ,$$ $$k_{xy}^{0}=0,k_{xxy}^{0}=0,k_{xyy}^{0}=0,k_{xxyy}^{0}=c_{s}^{4} \rho$$ $$K= \begin{bmatrix} 1 & 0 & 0 & -4 & 0 & 0 & 0 & 0 & 4 \\\\ 1 & 1 & 0 & -1 & 1 & 0 & 0 & 2 & -2\\\\ 1 & 0 & 1 & -1 & -1 & 0 & 2 & 0 & -2\\\\ 1 & -1 & 0 & -1 & 1 & 0 & 0 & -2 & -2\\\\ 1 & 0 & -1 & -1 & -1 & 0 & -2 & 0 & -2\\\\ 1 & 1 & 1 & 2 & 0 & 1 & -1 & 1 & -1\\\\ 1 & -1 & 1 & 2 & 0 & -1 & -1 & 1 & 1\\\\ 1 & -1 & -1 & 2 & 0 & 1 & 1 & 1 & 1\\\\ 1 & 1 & -1 & 2 & 0 & -1 & 1 & -1 & 1\\\\ \end{bmatrix}$$

我们开始着手构造碰撞算子：

$$\Omega \left( f \right) =K⋅g \\\\$$

目前，g是待求矩向量系数。

由于碰撞不会改变质量和动量，因此将其称为碰撞不变量，我们可以设置:

$$g_{0}=g_{1}=g_{2}=0 \\\\$$

对碰撞算子求矩,将其全部代入到Bolzmann演化方程，可推导得到：

$$g_{3}=\frac{w_{3}}{12} \left( \frac{2}{3} \rho + \rho \left( u_{x}^{2}+u_{y}^{2} \right) - \left( k_{xx}^{'}+k_{yy}^{'} \right) \right)$$ $$g_{4}=\frac{w_{4}}{4} \left( \rho \left( u_{x}^{2}-u_{y}^{2} \right) - \left( k_{xx}^{'}-k_{yy}^{'} \right) \right)$$ $$g_{5}=\frac{w_{5}}{4} \left( \rho u_{x}u_{y}-k_{xy}^{'} \right)$$ $$g_{6}=\frac{w_{6}}{4} \left( 2 \rho u_{x}^{2}u_{y}+k_{xxy}^{'}-2u_{x}k_{xy}^{'}-u_{y}k_{xx} \right) -\frac{1}{2}u_{y} \left( 3g_{3}+g_{4} \right) -2u_{x}g_{5}$$ $$g_{7}=\frac{w_{7}}{4} \left( 2 \rho u_{x}u_{y}^{2}+k_{xyy}^{'}-2u_{y}k_{xy}^{'}-u_{x}k_{yy} \right) -\frac{1}{2}u_{x} \left( 3g_{3}+g_{4} \right) -2u_{y}g_{5}$$ $$g_{8}=-2g_{3}-\frac{1}{2}u_{y}^{2} \left( 3g_{3}+g_{4} \right) -\frac{1}{2}u_{x}^{2} \left( 3g_{3}-g_{4} \right) -4u_{x}u_{y}g_{5}-2u_{y}g_{6}-2u_{x}g_{7}\\\\ +\frac{w_{8}}{4} ( \frac{1}{9} \rho +3 \rho u_{x}^{2}u_{y}^{2}- \left(k_{xxyy}'-2u_{x}k_{xyy}'-2u_{y}k_{xxy}'+u_{x}^{2}k_{yy}'+u_{y}^{2}k_{xx}'+4u_{x}u_{y}k_{xy}' ) \right)$$

其中， $ w{ \alpha }弛豫系数，w{4}=w_{5}=\frac{1}{ \tau} $ ，与粘性应力有关。其他可以根据实际情况进行调节。

算法验证-方腔流动

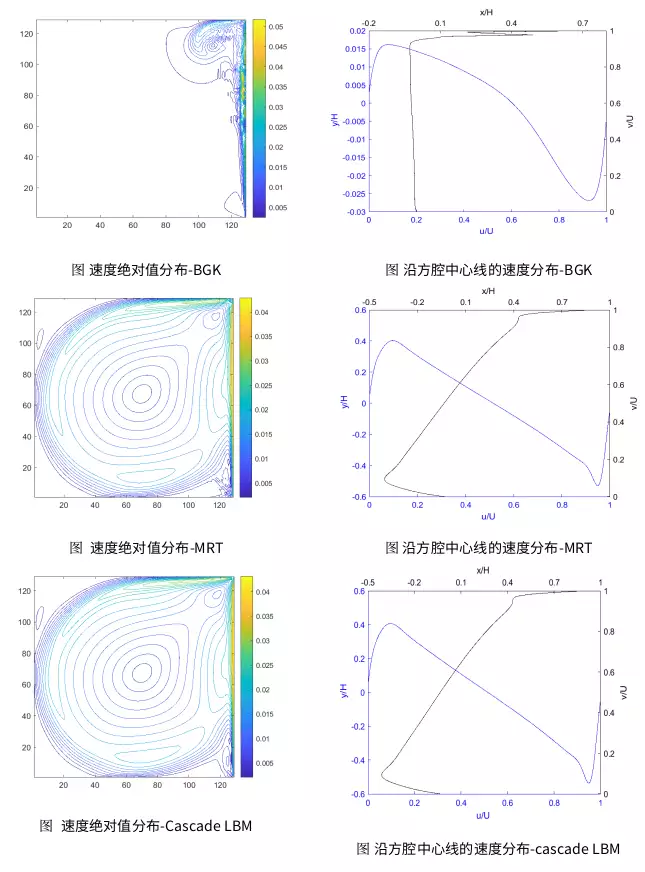
为对比上述BGK、MRT和Cascade LBM三个算法的性能，我们用广为熟悉的高雷诺数方腔流动进行验证。该算例网格数为128$\ast$ 128，相对较高的雷诺数Re为3200，排除压力的干扰，满足不可压条件，选择相对较低的顶盖的流动马赫数设为0.05。

在相同初始条件下，下图分别给出了三个算法的仿真结果。其中，左排为速度的绝对值分布，右排为中心线上的速度分布。对比三个结果，可以发现BGK在较少网格条件下无法收敛，而MRT和cascade LBM都能正常收敛，速度分布与其他论文结果一致¹⁸。细节上，MRT仿真的绝对速度，在右上边角和右下边角区域会出现微小的波动，这是由于这两个区域存在非常大的速度梯度，松弛算法的引入可能导致伽利略不变性的破坏，导致应力振荡。而cascade LBM较好的解决了这一问题。同时，需要注意的是，由于两个算法都采用相对较为稀疏的网格数，因此，均无法较好地模拟角区的流动细节。有不少文献也提出了一些解决办法。例如，对这些区域进行局部加密，或采用更高阶的算法，当然计算效率也会相应降低。

在接下的流固耦合仿真中，我们将采用cascade LBM算法，以增加算法的稳定性。

代码演示-LBM 算法 可视化 互动

请参考 shaderoty!

备注

最近可能重心没在这上面，有时间再解释每段代码的含义。

放这个主题的博客，一方面帮助把LBM方法作一个总结，另外，对于大量公式的博客提前练个手。

本博客公式编辑用mathjax， IDE用Typora，文档原先用是word写的，所以花了很大的精力将其匹配成markdown可识别的文字。

这里引入了一个工具：叫做docx2latex。其中不乏有很多需要调整的格式，主要是下划线_和^前面不能留有空格。

• TODO：

  公式自动编号；

  图片名称；

  Markdown重新转回到Latex格式；

¹. Frisch, U., B. Hasslacher, and Y. Pomeau, Lattice-gas automata for the Navier-Stokes equation. Physical review letters, 1986. 56(14): p. 1505. ↩

². McNamara, G.R. and G. Zanetti, Use of the Boltzmann equation to simulate lattice-gas automata. Physical review letters, 1988. 61(20): p. 2332. ↩

³. Higuera, F., S. Succi, and R. Benzi, Lattice gas dynamics with enhanced collisions. EPL (Europhysics Letters), 1989. 9(4): p. 345. ↩

⁴. Succi, S. and S. Succi, The lattice Boltzmann equation: for complex states of flowing matter. 2018: Oxford University Press. ↩

⁵. Timm, K., et al., The lattice Boltzmann method: principles and practice. Springer International Publishing AG Switzerland, ISSN, 2016: p. 1868-4521. ↩

⁶. Zhao, C., et al., Numerical study of natural convection in porous media (metals) using Lattice Boltzmann Method (LBM). International Journal of Heat and Fluid Flow, 2010. 31(5): p. 925-934. ↩

⁷. Chen, H., et al., Extended Boltzmann kinetic equation for turbulent flows. Science, 2003. 301(5633): p. 633-636. ↩

⁸. Gupta, A. and R. Kumar. Lattice Boltzmann simulation to study multiple bubble dynamics. in ASME International Mechanical Engineering Congress and Exposition. 2007. ↩

⁹. Peng, Y., C. Shu, and Y. Chew, Simplified thermal lattice Boltzmann model for incompressible thermal flows. Physical Review E, 2003. 68(2): p. 026701. ↩

¹⁰. Frapolli, N., S.S. Chikatamarla, and I.V. Karlin, Entropic lattice Boltzmann model for compressible flows. Physical Review E, 2015. 92(6): p. 061301. ↩

¹¹. Mousavi, S.E., et al., Simulation of droplet detachment from hydrophobic and hydrophilic solid surfaces under the electric field using Lattice Boltzmann Method (LBM). Journal of Molecular Liquids, 2020. 313: p. 113528. ↩

¹². Delbosc, N., Real-time simulation of indoor air flow using the lattice Boltzmann method on graphics processing unit. 2015, University of Leeds. ↩

¹³. Gressman, P. and R. Strain, Global classical solutions of the Boltzmann equation without angular cut-off. Journal of the American Mathematical Society, 2011. 24(3): p. 771-847. ↩

¹⁴. Bhatnagar, P.L., E.P. Gross, and M. Krook, A model for collision processes in gases. I. Small amplitude processes in charged and neutral one-component systems. Physical review, 1954. 94(3): p. 511. ↩

¹⁵. Qian, Y.-H., D. d’Humières, and P. Lallemand, Lattice BGK models for Navier-Stokes equation. EPL (Europhysics Letters), 1992. 17(6): p. 479. ↩

¹⁶. Ouderji, F.H., Cascaded Lattice Boltzmann Methods Based on Central Moments for Thermal Convection, Multiphase Flows and Complex Fluids. 2019: University of Colorado at Denver. ↩

¹⁷. Premnath, K.N. and S. Banerjee, Incorporating forcing terms in cascaded lattice Boltzmann approach by method of central moments. Physical Review E, 2009. 80(3): p. 036702. ↩

¹⁸. Ghia, U., K.N. Ghia, and C. Shin, High-Re solutions for incompressible flow using the Navier-Stokes equations and a multigrid method. Journal of computational physics, 1982. 48(3): p. 387-411. ↩

¹⁹. Peskin, C.S., The immersed boundary method. Acta numerica, 2002. 11: p. 479-517. ↩

²⁰. Roma, A.M., C.S. Peskin, and M.J. Berger, An adaptive version of the immersed boundary method. Journal of computational physics, 1999. 153(2): p. 509-534. ↩