Dynamical system and chaos

学习资料:

• MIT 公开课 -第11/12/13周课程

• simplearth

• https://www.youtube.com/watch?v=KmOzUkILGAQ&list=PLmU0FIlJY-Mle_2Q0mjVMuQh9aZHDzNoP

• https://drive.google.com/drive/folders/1kM9ko27wA5NvmZ8CxHIKygdi-klzW0UZ

学习目标：

• Dynamical system $(M,f)$: the space M of its possible states, and the law $f^t$ of their evolution in time.

• equilibria / fixed points

• Poincare map

• Explore the neighborhood by 线化 the flow； check the linear stability of its equilibria/ fixed points, their stability eigen-directions.

• Symmetry to simplify your problem

• Go global: train by partitioning the state space of 1-d maps. Label the regions by symbolic dynamics.

• Venture global distances across the system by continuing local tangent space into stable/ unstable manifolds. Their intersections partition the state space in a dynamically invariant way.

• Guided by this topological partition, compute a set of periodic orbits up to a given topological length.

Introducation

数学家亨利·庞加莱（HenriPoincaré）在试图描述三个天体在彼此的引力影响下的行为时首次遇到了”混乱“状态。事实证明，它们的运动很难预测，他称这种不稳定的运动为“混沌”。例如在不可压缩流动中，通过足够大的粘度稳定的层流状态的全局稳定的平衡性得以维持。随着粘度降低（雷诺数增加），湍流出现，以混沌状态空间轨迹表示。看似简单的混沌定义，大致基于类似于熵的量，即宇宙中事物从一种有序状态转变为一种无序状态的固有趋势。如果这个类似于熵的数字称为扩展熵，则该系统可能会变得混乱，而具有零扩展熵的系统则不会变得混乱。从本质上讲，使研究人员可以迅速捕捉事物迅速发展为不可预测深渊的趋势。

其特点可以总结：

• 长期行为很难或无法预测：即使是对混沌系统当前状态的非常精确的测量，也都无法指示系统的位置。必须再次测量系统以找出其位置。
• 对初始条件的敏感依赖（Poincare，Birkhoff甚至Turing指出的属性 ）：从非常接近的初始条件开始，混沌系统会迅速移动到不同的状态。
• 宽带频谱：混沌系统的输出听起来“嘈杂”。许多频率被激发。
• 错误的指数放大：在任何现实世界中，少量外部噪声都会迅速增长以控制系统。如果此噪声低于测量精度，则使实验者看不到或无法控制该噪声，则该系统似乎不可预测。微观的“热浴”被放大到人类规模。
• 局部不稳定性与全局稳定性：为了扩大小错误和噪声，行为必须是局部不稳定的：在短时间内，附近的状态会彼此远离。但是，为了使系统始终如一地产生稳定的行为，必须在很长一段时间内将一系列行为归为自身。这两个属性的张力导致结构非常优雅的混沌吸引子。

我感觉这门学科，是很多学科融合的新思想实践，包括信号处理、流体力学、热力学、统计数学、拓扑学和动力学等学科思想精华的集大成。从复杂的动力学问题中，化繁为简，提取有用的可解释性的物理特征或者相关结构。在Chaosbook这本书中,我们将学到the duality between the local, topological, short-time dynamically invariant compact sets (equilibrium, periodic orbits, partially hyperbolic invariant tori) and the global long-time evolution of densities of trajectories. 混沌动力学是由局部不稳定运动的相互作用以及整体稳定与不稳定流形的能量交换所产生。理解混沌的意义在于，如果以此为基础的invariant拓扑结构解释，那么后续的可观测结果，例如传感器测到的压力、频谱数据中的潜藏循环平稳信息也能进一步被挖掘、物理解释与理解。

闲话：pinball在书中被作为一个例子来解释Chaos，这是一个shadertoy的制作pinball的算法链接。

确定性系统本身是由初始条件完全决定。随机系统，除了初始条件以外，还受到噪声和其他控制的影响。从随机系统中寻找确定性是关键，也是难点。

• 如果一个确定性系统具有局部不稳定性(positive Lyapunov exponent) 和 globally mixing (positive entropy), 这个系统就成为是混沌的。

1. finite-time Lyapunov exponents

举一个例子，证明finite-time Lyapunov exponents在边界层分离识别的妙用：

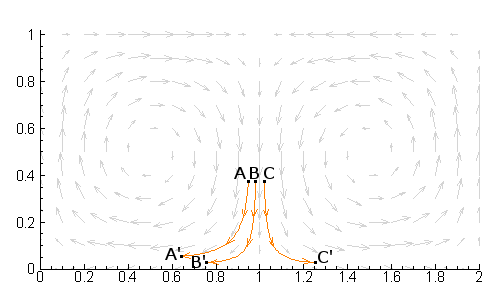
上图是一个实实在在的Plane Coututte的流体力学系统，在初始状态放置三个粒子A、B、C，在t时间后，观察到三个粒子的发展轨迹相互迥异。我们可以通过sensitivity来衡量这一不同的初始状态。

$$|\delta x(t)|\approx e^{\lambda t}|\delta x(0)|$$

其中，$\lambda$ ,代表系统轨迹的平均分离率，so called Lyapunov exponent. For any finite accuracy $\delta x=|\delta x(0)|$ of the initial data, the dynamics is predictable only up to a finite Lyapunov time

$$T_{Lyap}\approx -{1\over \lambda}ln|\delta x/L|$$

1. globally mixing (positive entropy)

在热力学中，混合熵是当几个初始分离的不同组分（总状态处于内部的热力学平衡），除去他们之间的化学反应，总熵增加，最后建立内部平衡的新的热力学状态的时间。

flows and maps

• A flow: the evolution rule $f^t$ can be used to map a region $M_i$ of the state space into the region $f^t(M_i)$.

  闲话1：Manifolds 在微分几何的课程中有非常精彩的介绍。sagemath软件也有集成关于流行symbolic运算的功能，感兴趣可以了解。

  闲话2： The ring of fire - 这个着色器渲染出的，加的是随机噪声, 非物理。

让我们来举一个例子：厨房的燃气灶的火焰，是在1855年有哥廷根化学天才Robert Bunsen发明的。它的火焰前部不稳定性可能是非线性系统最熟悉的例子之一，表现出“湍流”（时空混沌特性）。

这样一个例子可以用简单的Kuramoto-Sivashinsky system来近似(也许会包含一些系数)：¹

$${\partial u \over \partial t} + {1\over 2} {\partial u^2 \over \partial x} + {\partial ^2 u \over \partial x^2} + {\partial^4 u\over \partial x^4}$$

利用空间傅里叶变换：

$$C_n (t)= {1\over L} \int_0^L u(x,t) e^{-inKx}dx\\\\ u(x,t) = \sum_{n\in Z} C_n (t) e^{inKx}$$

其中，

$$K = 2\pi /L, C_{-n} (t)= C_n (t)^*$$

带入上面的主式：

$$\sum_{n\in Z}e^{inKx}[{dC_b(t)\over dt}+ C_n(t)\sum_{l\in Z}C_l(t) i l K e^{ilKx}- n^2 K^2 C_n(t) + n^4 K^4 C_n (t)]=0$$

通过Erik Teichmann²的公式（7）-（10）的推导，构造出与论文¹一样的形式:

$${dC_b(t)\over dt}+ \sum_{m\in Z}imKC_m(t)C_{n-m}(t)- n^2 K^2 C_n(t) + n^4 K^4 C_n (t)=0$$

要解这个非线性的公式貌似还没有这么简单，得用到所谓的ETD（exponential time differencing）算法², 这个算法解决某一类问题:

$${dc\over dt} = aC + F(C,t)$$

其中，a 是常数，F(C,t) 是非线性项。

具体的操作是，首先要对时间进行从$t_n -> t_n +h$积分，积分前要乘一个因子$e^{-ct}$:

$$C(t_{n+1})=C(t_n)e^{ah}+e^{ah}\int_0^h e^{-a\tau} F(C(t_n+\tau),t_n+\tau)d\tau$$

ETD方法的思想就是利用数值近似求解该方程。

• ETD1：一阶精度， 认为F恒定：local truncation error= $h^2 F_t /2$

  $$C_{n+1}= C_n e^{ah}+ F_n (e^{ah}-1)/a$$

• ETD2：二阶精度，$F= Fn + \tau (F_n -F{n-1})/h + O(h^2)$, local truncation error= $5 h^3 F_{tt}/12$

  $$\tilde{C}_n = C_n e^{ah} + F_n {e^{ah}-1 \over a}\\\\ C_{n+1}= \tilde{C}_n + {(F(\tilde{C}_n, t_n+h)-F_n)(e^{ah}-1-ah)\over a^2h}$$

• 再高阶的任意精度，见参考文献²

### 具体K-S代码如下：

#fork from https://github.com/boundter/kuramoto-sivashinsky
import numpy as np
import matplotlib.pyplot as plt


class Kur_Siv:
    def __init__(self, h, L, N, u0):
        self.C = np.fft.rfft(u0)
        self.N = N
        if self.N > self.C.size + 1:
            print("Too few fourier-modes for the Galerkin-Approximation")
        for i in range(N+1, self.C.size):
            self.C[i] = 0
        self.h = h
        self.K = 2*np.pi/L
        self.a = np.zeros(self.N)
        self.eah = np.zeros(self.N)
        for i in range(1, self.N + 1):
            self.a[i - 1] = i**2*self.K**2 - i**4*self.K**4
            self.eah[i - 1] = np.exp(self.a[i - 1]*h)
        self.modes = np.where(np.abs(self.a) > 1e-12)[0]
        self.a = self.a[self.modes]
        self.eah = self.eah[self.modes]

    def get_u(self):
        return np.fft.irfft(self.C)

    def calc_F(self, C): #非线性项计算
        F = np.zeros(C.size - 1, dtype=np.complex128)
        for i in range(1, self.N + 1):
            su = 0
            for j in range(-self.N + i, self.N + 1):
                if (i - j) < 0:
                    C_off = np.conjugate(C[j - i])
                else:
                    C_off = C[i - j]
                if j < 0:
                    C_norm = np.conjugate(C[-j])
                else:
                    C_norm = C[j]
                su += 1j*j*self.K*C_norm*C_off
            F[i - 1] = su
        return F

    def integrate(self):
        C_before = np.copy(self.C[self.modes + 1])
        F = self.calc_F(self.C[:self.N + 1])[self.modes]
        C_mid = np.copy(self.C[:self.N + 1])
  

if __name__ == "__main__":
    L = 2*np.pi
    N = 3*int(L/(2*np.pi))
    n = 41
    x = np.linspace(0., L, 200)
    y = np.cos(3*np.sin(x))
    kur = Kur_Siv(0.01, 8*np.pi, N, y)
    u = kur.get_u()
    result = [u]
    for i in range(0, n):
        kur.integrate()
        result.append(kur.get_u())
    plt.imshow(result, cmap='hot', interpolation='nearest')
    plt.show()

• 结果展示：为40个周向模态的幅值随时间分布的演化图

  

  除了最基本的主干部分，还一个添加一个velocity-field 计算函数：其功能是将所有周向模态叠加，转化回物理域。

  vector<double> KuramotoSivashinsky::GetU(Vector<double>* x){
      vector<double> u;
      for (int i = 0; i < (*x).size(); ++i){
          u.push_back(c[0].real());
          for (int j = 1; j < C.size(); ++j){
              u[i] += 2*C[j].real()*cos(j*K*(*x)[i]) - 2*C[j].imag()*sin(j*K*(*x)[i]); //乘2可能是模态正负对称，但只算了正模态
          }
      }
      
  }

  还可以添加particles进行观察：

  $${dX\over dt}= u(X,t)$$

  for (int i = 0; i < n; ++i) {
      kuramoto.Integrate();
      vector<double> u = kuramoto.Getu(&x);
      double t = kuramoto.Gett();
      fprintf(datafile, "%.4f ", t);
      for (int j = 0; j < number_particles; ++j) {
        x[j] += u[j]*h;
        if (x[j] < 0) x[j] += L;
        else if(x[j] > L) x[j] -= L;
        fprintf(datafile, " %.6f", x[j]);
      }

Nonlinear Dynamics: Stability and bifurcation YouTube

参考David P. Sanders，对分叉(一维)讲的特别到位。

链接: https://pan.baidu.com/s/1seEDWIW9TVnXnckRYKbgTA 密码: jp8d

类似讲座 https://www.youtube.com/watch?v=7mo1H_8nobM

https://www.youtube.com/watch?v=KmOzUkILGAQ&list=PLmU0FIlJY-Mle_2Q0mjVMuQh9aZHDzNoP

• 循环的工作原理1：离散动力系统理论简介（讲座）
• 循环的工作原理2：计算有效的离散动力学（讲座）

basic flow dynamical model

• Heat equation

$${\partial T\over \partial t} = -u {\partial T \over \partial x} -v {\partial T\over \partial y} +\kappa ({\partial^2 T\over \partial x^2} +{\partial^2T\over \partial Y^2}) + F$$

• Non-linear effects (Burger’s equation) 参考

  $${\partial u \over \partial t} = -u {\partial u\over \partial x} +\nu {\partial^2 u \over \partial x^2}$$

  Using the product rule, we can rewrite this as

  $${\partial u \over \partial t} =-{1\over 2}{\partial (u^2)\over \partial x} + \nu {\partial^2 u \over \partial x^2}$$

• 另外一些简单的模型，基本差分格式，julia算法参考³

• N-S 不可压方程

  $${\partial u \over \partial t}+ u\cdot \nabla u = - {1\over \rho }\nabla p + \nu \nabla^2 u\\\\ \nabla \cdot u = 0$$

  涡量：

  $$w = \nabla \times u$$

  setp1 : we can derivate the vorticity equation:

  $$\nabla \times {\partial u \over \partial t} + \nabla \times (u \cdot \nabla u) = - \nabla \times({1\over \rho}\nabla p) + \nabla \times \nu \nabla^2 w$$ $$\nabla \times \nabla({p\over \rho}) =0$$ $$u \cdot \nabla u = {1\over 2} \nabla(u\cdot u) - u\times(\nabla\times u) = \nabla({u^2\over 2} ) - u\times w$$

  那么，上面的第二项可以化为：

  $$\nabla \times (u \cdot \nabla u) = \nabla \times \nabla ({u^2\over 2})- \nabla \times u \times w = \nabla \times (w \times u)\\\\ =(u \cdot \nabla)w - (w\cdot \nabla)u + w(\nabla\cdot u) + u(\nabla \cdot w)$$

  上述的第二项为vortex stretching term，在二维中为0:

  $$(w \cdot \nabla)u = (w_x {\partial \over \partial x}+w_y{\partial \over \partial y}+w_z{\partial \over \partial z}) u =0, w_x=0, w_y = 0, w_z = w$$

  第一项叫做advection terms，也叫nonlinear Jacobian, 用streamfunction来代替：

  $$(u\cdot \nabla)w = u{\partial w \over \partial x}+v {\partial w \over \partial y} = {\partial \psi \over \partial y}{\partial w\over \partial x} - {\partial \psi \over \partial x}{\partial w\over \partial y}$$

  setp2: The vorticity equation for two-dimensional incompressible flow becomes:

  $${\partial w \over \partial t} + {\partial \psi \over \partial y}{\partial w\over \partial x} - {\partial \psi \over \partial x}{\partial w\over \partial y} = \nu ({\partial^2 w\over \partial x^2 }+{\partial^2 w\over \partial^2 y})$$

  Step3: the kinematic relationship between streamfunction and vorticity is given by Possion equation:

  $${\partial^2 \psi \over \partial^2 x} + {\partial^2 \psi \over \partial^2 y} = -w$$

The vorticity-streamfunction formulation has several advantages over solving N-S equation. It eliminates the pressure term from the momentum equation and hence, there is no odd-even coupling between the pressure and velocity.

Two-step time-stepping alogorithm

• Start from an inition condition w at t=0
• Invert the Possion equation to determine $\psi^n$
• Timestep the vorticity equation forward to determine $\psi^{t+1}$ from $w^t$ and $\psi^t$
• Go back to step 3 and repeat to find $w^{t+2}$ from $w^{n+1}$ and $\psi^{n+1}$

## 1.1 Setting up the discret grid and parameters
struct Grid
    N::Int64
    L::Float64

    ∇x::Float64
    ∇y::Float64

    x::Array{Float64, 2}
    y::Array{Float64, 2}

    Nx::Int64
    Ny::Int64

    function Grid(N, L)
        Δx = L/N #[m]
        Δy = L/N #[m]

        x = 0. -Δx/2.:Δx:L + Δx/2.
        x = reshape(x, (1,size(x,1)))
        y = -L -Δy/2.:Δy:L + Δy/2.
        y = reshape(y, (size(y,1), 1))

        Nx, Ny = size(x, 2), size(y, 1)

        return new(N, L, Δx, Δy, x, y, Nx, Ny)

    end
end

## set grid parameters
begin
    N = 30
    G = Grid(N, 1.)

    Δx = G.∇x
    Δt = 0.01

    δM = 0.05
    Re = 40
    δI = δM*Re^(1/3)

end

}

## inverting the Poisson equation for ψ
#  below， we use Jacobi iteration (introduced by Prof. Edelman and John Urschel earlier
#  in the class) to invert:
#  ξ = {∂^2 ψ \over ∂ x^2} + {∂^2 ψ \over ∂ y^2}

begin
    function jacobi_step(ψ::AbstractMatrix, ξ::AbstractMatrix, G::Grid)
        ψnew = zeros(size(ψ))
        ψnew[2:end-1, 2:end-1] =[
            ((ψ[j+1, i] + ψ[j-1, i] + ψ[j, i-1] + ψ[j, i+1])/4
              - ξ[j, i]*(G.∇x^2)/4)
              for j=2:size(ψ,1)-1, i=2:size(ψ,2)-1
        ]
        return ψnew
    end

    function poisson_solve!(ψ, ξ, G; ϵ=1e-6, num_steps=500, return_results=false)
        if return_results
            returns = []
        end
        for i in 1:num_steps
            ψtmp = jacobi_step(ψ, ξ, G)

            if return_results
                push!(returns, deepcopy(ψtmp))
            end

            if maximum(abs.(ψtmp - ψ)) < ϵ
                ψ[:,:] = ψtmp
                break
            end
            ψ[:,:] = ψtmp
        end

        if return_results
            return returns
        end
    end
end;

## Example: the Rankine vortex
# Throughout, we will use the Rankine vortex field to illustate the relationship
# between vorticity ξ, the streamfunction ψ, and the velocity (u,v)

begin
    ξ0 = zeros( G.Ny ,G.Nx)
    x0, y0 = 0.5, 0.0
    idx = ((G.x .- x0).^2 .+ (G.y .- y0).^2).^0.5 .<0.25
    ξ0[idx] .= 1
end;

## Let's test our Jacobi solver by inverting for ξ for ψ and then re-diagnosing 
#  ξ to see if we retrieve our input.

begin
    ψ0 = zeros(size(ξ0)) # initial guess is just zeros
    @elapsed results = poisson_solve!(ψ0, ξ0 , G, ϵ=1e-8, num_steps=1000, return_results=true)
    ξ0verify = diagnoseξ(ψ0, G)
end;

¹. G. Sivashinsky, “Nonlinear analysis of hydrodynamic instability in laminar flames I. Derivation of basic equations” Acta Astron. , 4 (1977) pp. 1177–1206 ↩

². Exponential Time Differencing for Stiff Systems, JCP-2002, S.M. Cox & P.C. Matthews ↩

³. CFD Julia: A Learning Module Structuring an Introductory Course on Computational Fluid Dynamics ↩

⁴. Fluid dynamics with Oceananigans.jl | Week 13 | MIT 18.S191 Fall 2020 | Ali Ramadhan ↩

草稿

Waleffe (1995, 1997) further developed these ideas into a ‘self- sustaining process theory’ that explains the quasi-cyclic roll-streak behavior in terms of the forced response of streaks to rolls, growth of streak instabilities, and nonlinear feedback from streak instabilities to rolls.

The preponderance of recurrent, coherent states in wall-bounded shear flows suggests
that their long-time dynamics lie on low-dimensional state-space attractors.

They improve on the POD models by capturing the linear stability of the
laminar flow and saddle-node bifurcations of non-trivial 3D equilibria consisting of rolls,
streaks, and streak undulations.

The work of Skufca et al. (2006), based on a Schmiegel
(1999) 9-variable model, offers an elegant dynamical systems picture, with the stable
manifold of a periodic orbit defining the basin boundary that separates the turbulent
and laminar attractors at Re < 402 and the stable set of a higher-dimensional chaotic
object defining the boundary at higher Re.

invariant manifolds

We compute a new equilibrium solution of plane Couette flow and the leading eigenvalues and eigenfunctions of known equilibria at this Re and c

the calculation of exact invariant solutions of the fully-resolved Navier-Stokes
equations.

(a) that coherent structures are the physical images of the flow’s least unstable
invariant solutions, (b) that turbulent dynamics consists of a series of transitions between
these states, and (c) that intrinsic low-dimensionality in turbulence results from the low
number of unstable modes for each state (Waleffe (2002)).