参考资料：

https://mblondel.org/teaching/autodiff-2020.pdf

18.337J / 6.338J：并行计算和科学机器学习

技术计算主要有两个分支：机器学习和科学计算。在过去的十年中，机器学习受到了很多炒作，例如卷积神经网络和TSne非线性降维等技术为新一代数据驱动的分析提供了动力。另一方面，许多科学学科通过微分方程建模进行大规模建模，着眼于描述科学定律的随机微分方程和偏微分方程。

但是，这两个学科最近融合在一起。科学机器学习这个领域一直在展示一些结果，例如如何使用神经网络加速偏微分方程的仿真。已经开始专门开发新方法，例如概率编程和微分编程，以增强该领域的工具。但是，该领域的技术将计算和数值实践的两个巨大领域结合在一起，这意味着这些方法足够复杂。您如何反向传播由神经网络定义的ODE？您如何进行科学模拟器的无监督学习？

在本课程中，我们将深入研究这些方法，并了解它们的作用，制造原因，以及如何在各个领域整合数值方法，以突出其利弊，同时减轻其弊端。本课程将对数字技术进行一次调查，展示多少门学科以不同的名称从事同一工作，并使用一种通用的数学语言来导出有效的例程，以捕获数据驱动和基于机械的建模。

但是，如果天真地编码，这些方法将很快遇到扩展问题。为了解决这个问题，所有工作都将重点放在性能工程上。我们将从关注本质上是串行的算法开始，并学习优化串行代码。然后，我们将展示如何通过多线程和分布式计算技术（如MPI）并行处理逻辑繁重的代码，而直接的数学描述可以通过GPU计算并行化。

课程的最后一部分将是一个独特的项目，将这些技术结合在一起。作为一个新领域，学生将接触到“垂头丧气的果实”，并被引导到可以迅速产生影响的领域。在最后的项目中，学生将联手解决科学机器学习领域的新问题，并获得帮助撰写有关其工作的出版物质量分析。

一些资料：

微分编程：https://zhuanlan.zhihu.com/p/105662113

最终项目

最终项目是使用SIAM数值分析期刊 （或类似刊物）中的样式模板的10-20页论文。最终项目必须以其他人可以使用的形式包含用于算法的高性能（或并行化）实现的代码。期望进行全面的性能分析。根据学术评论文章（例如，阅读SIAM评论和类似期刊作为示例）对论文进行建模。

一种可能是复习本课程中未涵盖的有趣算法，并开发出高性能的实现。一些示例包括：

适用于Navier-Stokes等特定PDE的高性能PDE求解器
常见的高性能算法（例如：PDE的免费Jacobon-Free Newton Krylov）
在生物学，药理学或气候科学等领域进行参数敏感性研究
增广神经常微分方程
神经跳跃随机微分方程
平行模板计算
分布式线性代数核
统计库的并行实现，例如生存统计或大数据的线性模型。这是一个并行库示例）和第二个示例。
数据分析方法的并行化
稀疏线性代数方法的类型通用实现
快速的正则表达式库
数学库原语（exp，log等）

另一种可能性是进行最先进的性能工程。这将实现新的自动并行化或性能增强。对于这些类型的项目，不需要实施用于基准测试的应用程序，而是可以对已经存在的代码进行基准测试，以找出有利的情况（或导致性能下降）。可能的示例是：

创建一个用于数组操作的自动多线程并行化的系统，并查看哪种包最终会更有效
使用PARTR后端设置BLAS 并研究下游对多线程代码的影响，例如现有的PDE求解器
研究多线程循环中的工作窃取效果
快速并行类型通用FFT。史蒂芬·约翰逊（FFTW的创建者）和马英博的入门代码可在此处找到
类型通用BLAS。入门代码可以在这里找到
并行映射减少方法的实现。例如，对此的pmapreduce 扩展会pmap添加并行压缩，或者基于GPU的快速map-reduce。
使用诸如CUDAnative和/或 GPUifyLoops之类的工具研究将完整的软件包代码自动编译到GPU 。
研究数据库和数据框的替代实现。 DataFrames的NamedTuple后端，其他类型稳定的DataFrames，用于CSV读取的默认值以及其他大表格式（如JuliaDB）。

此外，科学机器学习是一个广阔的领域，有很多低落的果实。代替评审，可以将合适的研究项目用于最终项目。可能性包括：

微分方程伴随的加速方法
物理信息神经网络的改进方法
神经微分方程的新应用
大型ODE系统的并行隐式ODE求解器
适用于小型系统的GPU并行ODE / SDE求解器

最终项目主题必须在10月30日之前声明，并附上一页摘要。

主题表

每个主题由三部分组成：数值方法，性能工程技术和科学应用。这三个一起构成了一个完整的可用程序，并进行了演示。

科学模拟器的基础知识（第1-2周）
- 什么是科学机器学习？
- 优化序列号。
- 离散和连续动力系统简介。
并行计算入门（第2-3周）
- 并行形式和应用
- 并行微分方程求解器
- 通过多线程优化局部并行
- 您应该知道的线性代数库

作业1：并行动力学系统仿真和ODE积分器

连续动力学（第4周）
- 常微分方程是生态学，牛顿力学及其他领域的语言。
- 非刚性常微分方程的数值方法
- 刚度的定义
- 有效求解刚性常微分方程
- 发育生物学和生态学中生化相互作用产生的刚性微分方程
- 将类型系统和通用算法用作数学工具
- 前向自动微分求解f（x）= 0
- 基质着色和稀疏区分

作业2：动态系统中的参数估计和并行性开销

反问题和可微编程（第6周）
- 反问题的定义及其在临床药理学和智能电网优化中的应用
- 快速梯度的伴随方法
- 通过反向模式自动区分（反向传播）实现自动伴随
- 微分方程的伴随
- 使用神经常微分方程作为记忆有效的RNN进行深度学习
神经网络和基于数组的并行性（第8周）
- 数值线性代数中的缓存优化
- 通过数组操作实现并行
- 如何为GPU优化算法
分布式并行计算（Jeremy Kepner：7-8周）
- 并行形式
- 使用分布式计算与多线程
- 消息传递和死锁
- Map-Reduce作为分布式并行性的框架
- 使用MPI实现分布式并行算法

作业3：训练神经常微分方程（使用GPU）

物理信息神经网络和神经微分方程（第9-10周）
- 自动发现微分方程
- 用神经网络求解微分方程
- PDE的离散化
- 神经网络的基础和定义
- 卷积神经网络与PDE之间的关系
概率编程，程序的贝叶斯估计（第10-11周）
- 优化与贝叶斯方法之间的联系：贝叶斯后验与MAP优化
- 马尔可夫链蒙特卡罗方法简介
- 哈密顿蒙特卡洛只是辛辛的ODE求解器
- 通过后验参数估计的不确定性量化
全球化对模型的理解（第11周至第12周）
- 全局敏感性分析
- 全局优化
- 替代模型
- 不确定度量化

家庭作业

讲座摘要和讲义

请注意，讲座按主题分类，而不是按天细分。有些讲座多于1节课，有些则少。

第1课：简介和课程提纲

讲座与笔记

介绍和课程提纲（讲座）

这是为了确保我们都在同一页面上。它涵盖了课程提纲以及整个课程对您的期望。如果您尚未加入Slack，请使用介绍电子邮件中的链接（如果需要此链接，请给我发电子邮件！）。

讲座1.1：Julia入门

讲座与笔记

可选的额外资源

如果您对Julia还是不满意，这里有一些资源可以帮助您快速入门：

一些更深层次的材料：

1 2	julia> Threads.nthreads() win:12;ubuntu:24;

第2课：优化串行代码

讲座与笔记

在Julia 1中优化串行代码：内存模型，变异和向量化（讲座）文档

pkg> add BenchmarkTools
A = rand(100,100)
B = rand(100,100)
C = rand(100,100)
using BenchmarkTools
function inner_rows!(C,A,B)
  for i in 1:100, j in 1:100
    C[i,j] = A[i,j] + B[i,j]
  end
end
@btime inner_rows!(C,A,B)

Tip：

Heap allocation 需要一些时间，相比stack要快的多；
Mutation to Avoid Heap Allocations 函数后加“！”；
Julia Broadcasting mechanism；可大大提高performance，至少3倍
减少heap内存分配；
loop 损耗；
方程算子整体操作，一行代码；
heap allocation from slicing： A[50,50], @btime @view A[1:5,1:5] 只不过移动指针，没有创造内存，但如果没有@view，则需要创建内存
c ， c++比较快的一大原因是，全部指定type，这样，程序就可以提前编译打包，运行的时也无后顾之忧。julia虽然没有这么做，但也有一套打包成函数的机制。

julia分发机制（多态）：ff(x::Int,y::Int) = 2x + y； ff(x::Float64,y::Float64) = x/y； @show ff(2,5)； @show ff(2.0,5.0)

function vectorized!(tmp, A, B, C)
  tmp .= A .* B .* C
  nothing
end
function non_vectorized!(tmp, A, B, C)
  @boundscheck A, B, C #保证不越界修改内存，否则会导致计算机出错
  @inbounds for i in length(tmp) #这样的for循环速度和上面的一样，在julia中，for循环速度很快，如果不用check bounds的话
    tmp[i] = A[i] * B[i] * C[i]
  end
  nothing
end
  
@btime vectorized!(tmp, A, B, C) ->3.7us
@btime non_vectorized!(tmp, A, B, C)->9.4us

在Julia 2中优化串行代码：类型推断，函数专门化和调度（讲座）

优化序列号（注释）

可选的额外资源

在开始并行化代码，构建庞大的模型并自动学习物理学之前，我们需要确保我们的代码“良好”。您怎么知道您正在编写“好的”代码？这就是本讲座要回答的内容。在本讲座中，我们将介绍编写良好的串行代码并检查代码是否有效的技术。

第3课：通过物理信息神经网络进行科学机器学习的简介

科学机器学习简介1：作为函数逼近的深度学习（讲座）文档

科学机器学习简介2：物理信息神经网络（讲座）

$x''= -kx +0.1sin(x)$

# 通过DifferentialEquation求解
using Plots
using DifferentialEquations
k = 1.0
force(dx,x,k,t) = -k*x +0.1sin(x)
prob = SecondOrderODEProblem(force,1.0,0.0,(0.0,10.0),k)
sol = solve(prob)
plot(sol, label=["velocity" "Position"])

plot_t = 0:0.01:10
data_plot = sol(plot_t)
positions_plot = [state[2] for state in data_plot]
force_plot = [force(state[1],state[2],k,t) for state in data_plot]

# Generate the dataset
t = 0:3.3:10
dataset = sol(t)
position_data = [state[2] for state in sol(t)]
force_data = [force(state[1],state[2],k,t) for state in sol(t)]

plot(plot_t,force_plot,xlabel="t",label="True Force")
scatter!(t,force_data,label="Force Measurements")

NNForce = Chain(x -> [x],
           Dense(1,32,tanh),
           Dense(32,1),
           first)

1 2	loss() = sum(abs2,NNForce(position_data[i]) - force_data[i] for i in 1:length(position_data)) loss()

通过物理信息神经网络进行科学机器学习简介（注）

可选的额外资源

做科学机器学习（4小时研讨会）

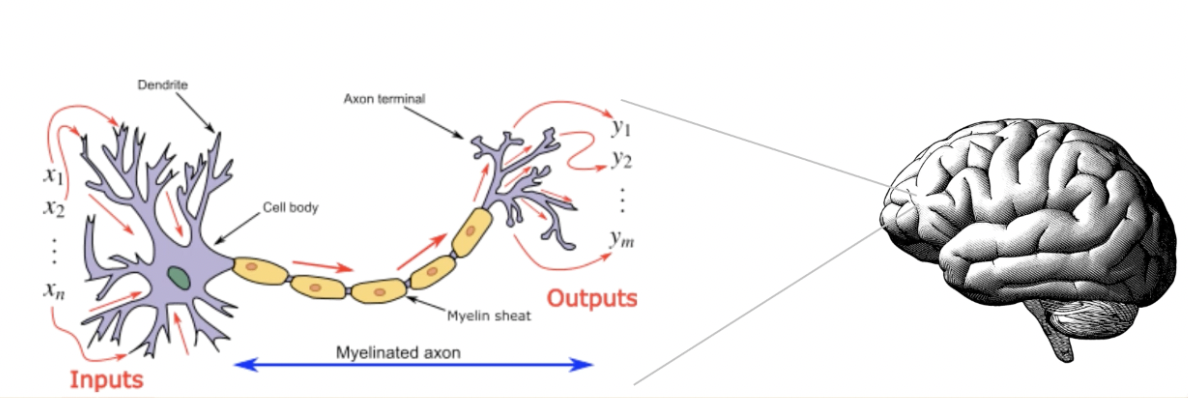
现在，让我们首先来看看应用程序：科学机器学习。什么是科学机器学习？我们将通过研究人们采用的几种方法以及使用科学机器学习解决的问题类型来定义领域。将介绍科学机器学习的领域及其在计算科学到气候建模和航空航天中的应用的跨度。将以各种名称介绍将要研究的方法，并列出该学科中出现的一般公式：将诸如微分方程之类的科学模拟工具与诸如神经网络之类的机器学习原语结合在一起通过微分编程来实现以前不可能的结果。做完调查后

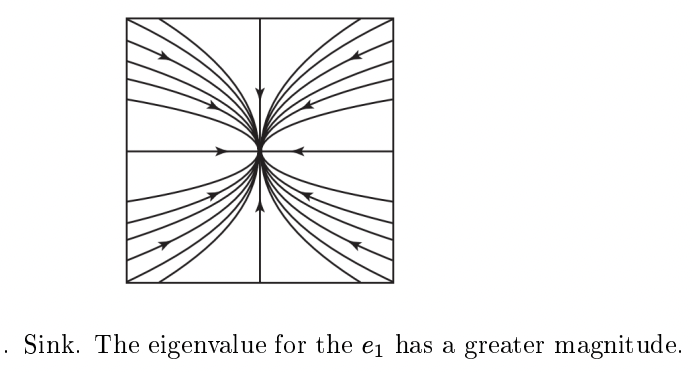
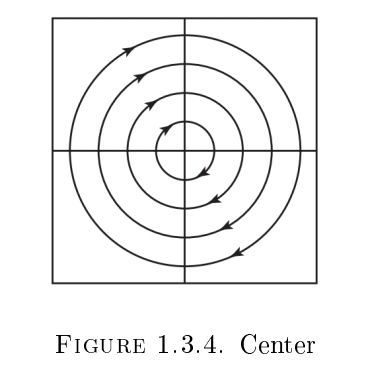
讲座4：离散动力系统简介

可选的额外资源

现在已经准备好阶段，我们看到要更深入地了解，我们将需要很好地了解离散和连续动力学系统是如何工作的。我们将从开发科学模拟器的基础开始：微分和差分方程。快速研究微分方程和差分方程的几何结果将为理解非线性动力学奠定基础，我们将快速转向数值方法来可视化。即使没有动力学系统的解析解，也可以通过渐近方法和线性化确定总体行为，例如收敛到零。稍后我们将看到这些相同的技术为微分方程数值方法的分析奠定了基础，例如Runge-Kutta方法和Adams-Bashforth方法。

由于微分方程的离散化确实是一个离散的动力系统，因此我们将以此为案例研究如何优化串行标量重代码。SIMD，就地操作，广播，堆分配和静态数组将用于获取用于动态系统仿真的快速代码。然后，这些模拟将用于揭示动力系统的一些有趣特性，在本课程的其余部分中将进一步探讨这些特性。

第5课：基于数组的并行，尴尬的并行问题和数据并行：单节点并行计算的基础

可选的额外资源

CPU运行成本图

现在我们有了一个具体的问题，让我们开始研究使其解决方案并行化的方法。首先，我们将看到许多系统几乎具有通过数组操作进行并行化的方式，我们将其称为基于数组的并行性。将讨论轻松并行化大块线性代数的能力，以及像OpenBLAS，Intel MKL，CuBLAS（GPU并行性）和Elemental.jl之类的库。这给出了一种方法内并行的形式，我们可以使用它来优化利用线性的特定算法。并行化的另一种形式是对输入进行并行化。我们将描述这是一种数据并行性的形式，并将其用作引入共享内存和分布式并行性的框架。将讨论这些并行化方法与应用程序注意事项之间的相互作用。

第6讲：并行方式

在这里，我们通过对并行化类型进行高级概述来继续描述并行化方法。SIMD和多线程被视为并行性的基本形式，其中消息传递是无关紧要的。然后介绍了加速器，例如GPU和TPU。进一步介绍了分布式并行计算及其模型。我们将看到的是，我们实际上正在执行哪种并行性并不是决定我们如何考虑并行性的主要决定因素。相反，决定因素是并行编程模型，在所有不同的硬件抽象中只能看到少数模型，例如基于任务的并行性或SPMD模型。

第7课：常微分方程：应用和离散化

在本讲座中，我们将描述常微分方程，它们在科学环境中出现的位置以及如何求解它们。我们将看到，了解数值方法的属性需要了解从逼近到连续系统生成的离散系统的动力学，因此，数值方法的稳定性直接与动力学的稳定性有关。这给出了刚度的概念，这是关于病态系统的更大的计算思想。

第8课：前向模式自动微分

通过高维代数进行正向模式自动微分（AD）（讲座）利用Dual的性质计算雅可比矩阵（非常有意思！🉑️）
通过高维代数的正向模式自动微分（AD）（注）

roundoff error

考虑到数值误差的引入。

Dual用来自动微分

https://github.com/JuliaDiff https://arxiv.org/pdf/1607.07892.pdf

Multidimensional dual number

$f(x+\sum_{i=1}^k y_i\epsilon_i)=f(x) + f'(x)\sum_{i=1}^k y_i \epsilon_i$

Where $\epsilon_i \epsilon_j =0$.

$\vec{x} = \begin{vmatrix} x_1 \\ \vdots \\ x_i \\ \vdots \\ x_k \end{vmatrix} \rightarrow \vec{x}_\epsilon = \begin{vmatrix} x_1+\epsilon_1 +0\sum_{n=2}^k \epsilon_n \\ \vdots \\ x_i+\epsilon_i +0\sum_{n\neq i} \epsilon_n \\ \vdots \\ x_k+\epsilon_k +0\sum_{n=1}^{k-1} \epsilon_n \end{vmatrix}=\begin{vmatrix} x_1+\epsilon_1 \\ \vdots \\ x_i+\epsilon_i \\ \vdots \\ x_k+\epsilon_k \end{vmatrix} \rightarrow f(\vec{x}_\epsilon)=f(\vec{x})+\sum_{i=1}^k {\partial f(\vec{x})\over \partial x_i} \epsilon_i$

struct Dual{T}
    val::T   # value
    der::T  # derivative
end
Base.:+(f::Dual, g::Dual) = Dual(f.val + g.val, f.der + g.der)
Base.:+(f::Dual, α::Number) = Dual(f.val + α, f.der)
Base.:+(α::Number, f::Dual) = f + α

#=
You can also write:
import Base: +
f::Dual + g::Dual = Dual(f.val + g.val, f.der + g.der)
=#

Base.:-(f::Dual, g::Dual) = Dual(f.val - g.val, f.der - g.der)

# Product Rule
Base.:*(f::Dual, g::Dual) = Dual(f.val*g.val, f.der*g.val + f.val*g.der)
Base.:*(α::Number, f::Dual) = Dual(f.val * α, f.der * α)
Base.:*(f::Dual, α::Number) = α * f

# Quotient Rule
Base.:/(f::Dual, g::Dual) = Dual(f.val/g.val, (f.der*g.val - f.val*g.der)/(g.val^2))
Base.:/(α::Number, f::Dual) = Dual(α/f.val, -α*f.der/f.val^2)
Base.:/(f::Dual, α::Number) = f * inv(α) # Dual(f.val/α, f.der * (1/α))

Base.:^(f::Dual, n::Integer) = Base.power_by_squaring(f, n)  # use repeated squaring for integer powers

h(x) = x^2 + 2
a = 3
xx = Dual(a, 1)
h(xx)

#derivative(f, x) = f(Dual(x, one(x))).der

Jacobian：

就像我们将很快看到的那样，计算导数的能力是科学计算和机器学习中很多问题的基础。我们将在后面的讲座中具体看到它，它针对刚性常微分方程求解器的隐式方程f（x）= 0的求解，以及在拟合神经网络中的应用。这样做的常见高性能方式称为自动区分。本讲座介绍了正向和反向模式自动微分的方法，以设置该技术的未来研究用途。

参考：

forwardDiff-2016
forwardDiff-2017

第9课：求解刚性常微分方程

演讲笔记

求解刚性常微分方程（讲座）
求解常微分方程（注） https://nextjournal.com/pkj-m/a-summer-with-jacobians

Newton’s method and Jacobians

Implicit Euler method (for non-stiff ODE and also stiff ODE)

If we wanted to use this method, we would need to find out how to get the value $u_{n+1}$ when only knowing the value $u_n$. 首先，将方程移项：

and now we have a problem:

通过牛顿法迭代：

Where $J(x_k)$ is the Jacobian of g at the point $x_k$.

该过程在实际操作中，分为两步：
- Solve Ja=g（x_k） for a
- Update x_{k+1}= x_k -a
实际在求解a的过程，更是有很多技巧，比如需要J稀疏化。当然还要于之前学到的auto forward derivation挂钩,以快速求解雅可比矩阵。最终目的是提高求解效率。

After the J has been computed by forword-mode AD, we need to solve a linear equation $Ja=b$. 数学形式上来说，可以通过求J的逆矩阵来解方程。针对稀疏矩阵J来说，应该有更高效的算法（小稀疏矩阵）：

另外一种方法（针对大稀疏矩阵）：Jacobian-Free Newton Krylov technique

关于牛顿法收敛性的补充读物

解决刚性的常微分方程，特别是那些由偏微分方程引起的常微分方程，是科学计算的常见瓶颈。规模最大的科学计算模型通常使用大量的计算能力，以解决一些隐式的时间步长PDE解决方案！因此，我们将深入探讨如何结合使用不同的方法来创建一个刚性的常微分方程求解器，并研究Jacobian计算和线性求解的不同方面以及它们的效果。

讲座10：基本参数估计，反向模式AD和反问题

优化问题

首先需要构建cost function,比如L2 类型：

$C(p)= \sum_i^N\left\Vert f(x_i;p)-y_i \right\Vert$

寻找最优的p使得C最小。

求解上述最优化问题，最常用的办法为梯度下降法（牛顿法）：

$p_{i+1}=p_i -({d\over dp}{dC\over dp})^{-1}{dC\over dp}$

试图逼近梯度的最小值点：

${dC\over dp}=0$

其中，${d\over dp}{dC\over dp}$被称为Hessian matrix, 为梯度的雅可比。但对于复杂问题来说，计算量相当大。

事实上，该求解最优化问题和求解ODE有紧密的联系：

$p' = -{dC\over dp}$

求解上述ODE，利用上一节的Implicit Euler method方法：

$p_{i+1}=p_i - \alpha {dC(p_{i+1})\over dp}$

整理到同一边，得到g, 再通过牛顿法迭代：

$p_{k+1}=p_k -({d\over dp}{dC\over dp})^{-1}g(x_k)$

同样的，需要求解Hessian 矩阵。

神经网络求解优化问题

$NN_3(x)= W_3\sigma_2. (W_2\sigma_1.(W_1x+b_1)+b_2)+b_3)$ $C(p)= \sum_k^N \left\Vert DNN(x_k;p)-f(x_k)\right\Vert\\\\ p=[W_i,b_i]$

训练神经网络，得到参数，使得cost function最小。

Recurrent Neural Networks

$x_{k+1}=x_k + DNN(x_k,k;p)$

实际上，可以写成类似ODE的形式，称为neural ODE：

$x' = DNN(x,t;p)$

计算要素: $df(x_i)\over dp}$

利用chain rule：

${dC\over dp}=\sum_i^N 2(f(x_i;p)-y_i){df(x_i)\over dp}$

${df(x_i)\over dp}$的计算需要优化，可以通过之前学的Forward-Mode Automatic Differentiation。

如果是神经网络模型，f用CNN来替代，那么同样要求神经网络模型的针对p参数$W_i,b_i$的梯度。pytorch类似的框架就是干这些活。

对于大量的数据点，Forward-Mode Automatic Differentiation 计算量可能会很大。因此，有必要进行优化。

更有效的，或者目前的神经网络常用的方法是backpropagtion。具体参考blog-machine learning 基础篇“如何求backprogation？” 本质是charin rule。

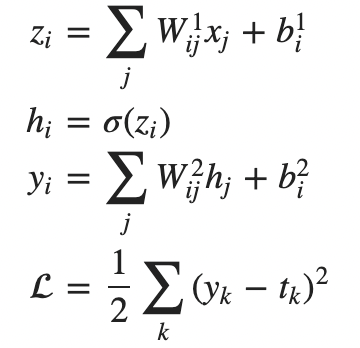
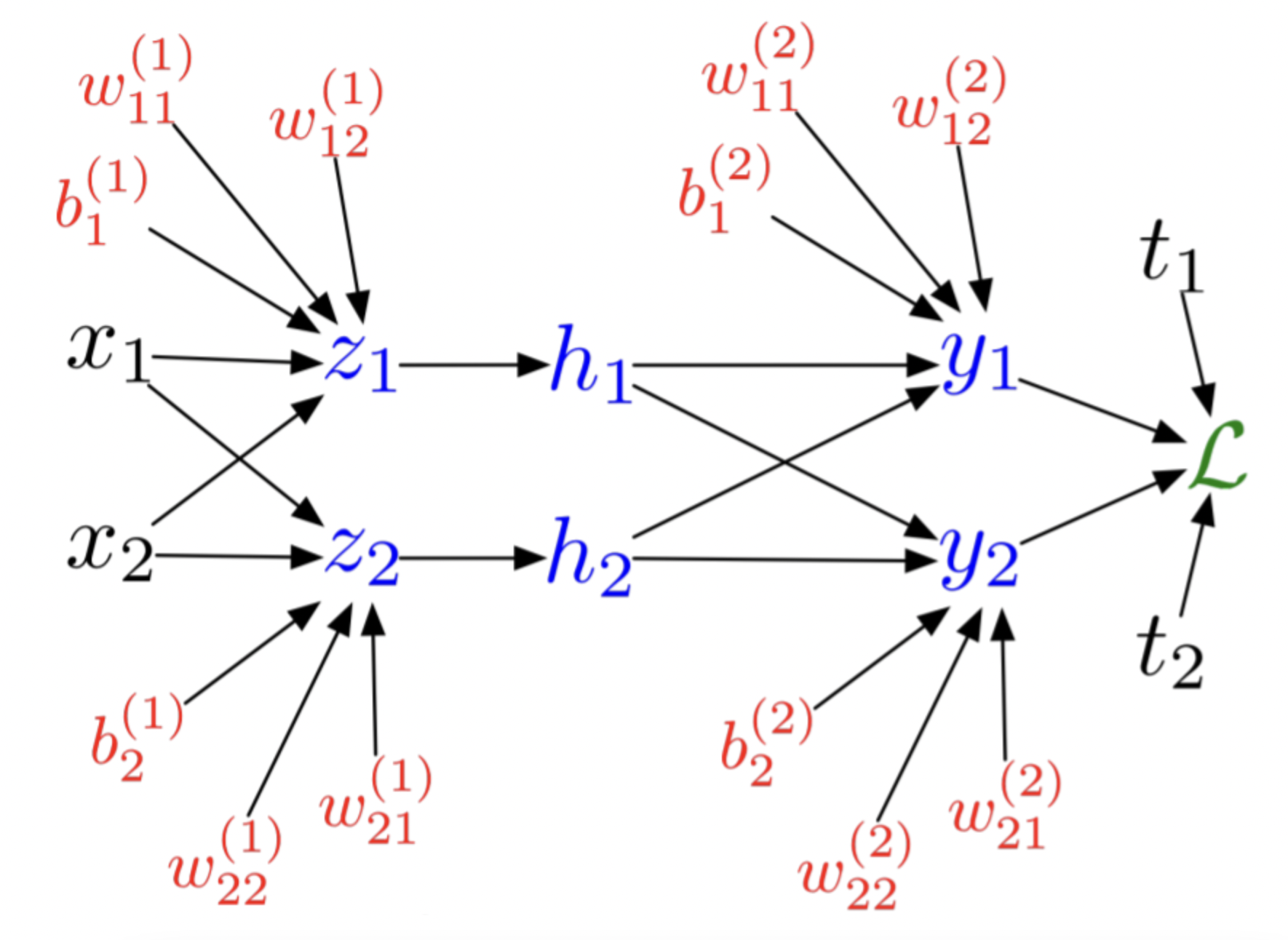
整理成矩阵相乘的形式：

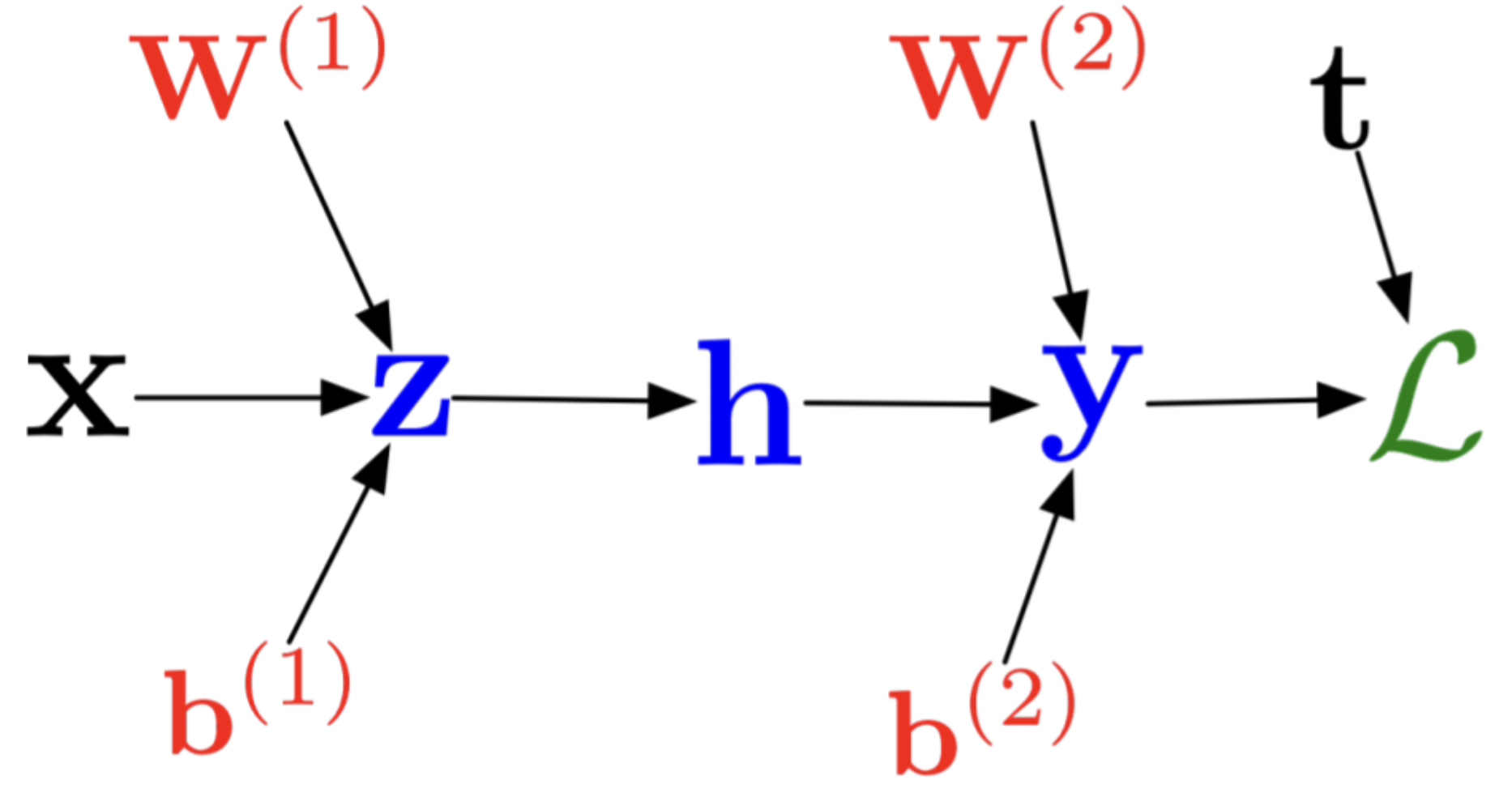
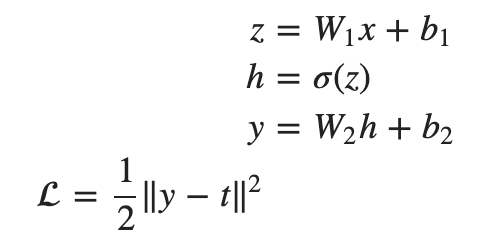
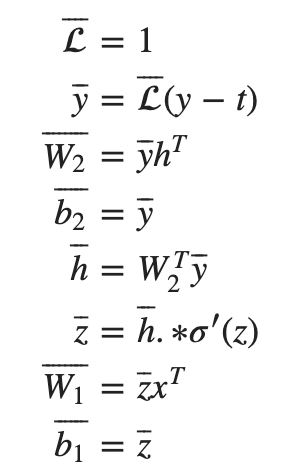
最后总结DNN的链式法则：

$r_i = W_iv_i+b_i\\\\ v_{i+1}=\sigma_i.(r_i)\\\\ v_1 = x\\\\ v_n = y\\\\ L={1\over 2}\Vert y-t\Vert\\\\ reverse \space rule:\\\\ \overline{L} =1\\\\ \overline{v_n} = \overline{L}(y-t)\\\\ \overline{v_i}=W_i^T \overline{r_i} \\\\ \overline{W_i}= \overline{r_i} v_i^T \\\\ \overline{b_i}= \overline{r_i}\\\\ \overline{r_i}=\overline{v_{i+1}}.*\sigma_i'(r_i)$

Reverse-Mode Automatic Differentiation

$f=f^L\circ f^{L-1}\circ ....\circ f^{1}\\\\ f(x)=f_L(f_{L-1}(...(f_1(x))))\\\\ f'(x)=f'_L(x)f'_{L-1}(x)f'_{L-2}...f'_1(x)\\\\$

Forward AD可以写成：

$Jv = J_LJ_{L-1}...J_1v$

前向AD利用 Dual number高效求解,Jv。

Reverse AD (backpropagation):

$v^TJ =v^TJ_LJ_{L-1}...J_1\\\\ same: (v^TJ)^T=J^Tv=J_1^TJ_2^T...J_{L-1}^TJ_{L}^Tv$

we go forwards and then push back the Jacobian transform at each step mutiplied the bar (the vector v)

对应的，后向AD利用pushback function高效求解,v^TJ。

$if \space y=[y_1,y_2,...]=f(x_1,x_2,...),\\\\ then \space [\overline{x_1},\overline{x_2},...]=\mathcal{B}_f^x(\overline{y})\\\\ \overline{x_i}=\sum_i \overline{y_i}{\partial y_i\over \partial x_i}=\mathcal{B}_f^x(\overline{y})$

再次理解计算要素：利用上述关系，如何求雅可比矩阵：

$J={df\over dx}= \begin{bmatrix} {\partial f_1\over \partial x_1} & {\partial f_1 \over \partial x_2}& \cdots & {\partial f_1\over \partial x_n} \\ \partial f_2\over \partial x_1& & \cdots & \\ \vdots & &\ddots & \vdots \\ {\partial f_n \over \partial x_1} & & \cdots & {\partial f_n\over \partial x_n} \end{bmatrix}$

雅可比的每一项都可以理解为只在p_i 参数起作用时，对整体的影响：

$J e_i = J_i (\space i^{th} \space column \space of J) --> forward \space AD\\\\ J^T e_i = J_i (\space i^{th} \space row \space of J) --> reverse \space AD\\\\$

我们来解释之前的链式法则的推导，其中最后一步$\overline{L}=1$可以写成雅可比与v相乘的形式：

$J^T v={df\over dx}v=[{\partial f_1\over \partial x_1} \space {\partial f_1\over \partial x_2} \space ... \space {\partial f_n\over \partial x_n} ]\begin{bmatrix} 1\\1\\ \vdots \\ 1 \end{bmatrix}= {\partial f_1\over \partial x_1} + {\partial f_1\over \partial x_2} + ... \space {\partial f_n\over \partial x_n}$

这表明reverse AD 可以计算gradient。

最终，Hessians are the Jacobian of the gradient。首先通过reverse AD计算gradient ${dC\over dp}$,然后通过forward AD 得到H的 vector product。

$Hv=({dC\over dp})'v$

对比Forward和backward AD：

Forward AD evaluates chain rule from right (inner function) to left (outer function)
Reverse AD evaluetes chain rule from left (outer function) to right (inner function)
Output_dimension > input_dimension || input_dimension<< code_size -> Use forward AD
Output_dimension < input_dimension && input_dimension>>code_size -> Use reverse AD

单标量的拉回给出函数的梯度，而使用对偶的正向模式的前推给出方向导数。正向模式计算雅可比行列，而反向模式计算梯度（雅可比行行）。因此，两种方法的相对效率基于雅可比行列式的大小。如果f：Rn→Rm，则雅可比行列的大小为m×n。如果m远小于n，则每行的计算速度会更快，因此使用反向模式。在渐变的情况下，m = 1，而n可以很大，从而导致这种声音。同样，如果n远小于m，则按每一列进行的计算将更快。不久我们将看到反向模式AD相对于正向模式具有较高的开销，因此，如果值相对相等（或n和m小），则正向模式会更有效。

现在我们有了模型，您如何使模型适合数据？本讲座讲解了用于参数估计的基本射击方法，展示了其等效于训练神经网络的方法，并深入讨论了如何在训练过程中利用反向模式自动微分来有效地计算梯度。

参考：

chainrule
火箭控制🚀-JUMP
https://roberttlange.github.io/posts/2019/08/blog-post-6/
What is Automatic Differentiation? 非常好！一点要看！🐶
https://arxiv.org/pdf/1502.05767.pdf
Zygote ：什么是pushback

第11课：可微编程和神经微分方程

案例1: 线性方程

$A_{M\times M}x(p)=b(p)\\\\ {dg\over d p}={\partial g\over \partial p}+{\partial g \over \partial x}{\partial x\over \partial p}\\\\ x_{p_i}=A^{-1}(b_{p_i}-A_{p_i}x)$

为计算$dg\over dp$, 难点是第二项：

$g_xx_p=\underbrace{g_x}_{1\times M}[\underbrace{A^{-1}}_{M\times M}\underbrace{(b_p-A_p x)}_{M\times P}]=\underbrace{[g_x A^{-1}]}_{1\times M}\underbrace{(b_p -A_p x)}_{M\times P}$

引入adjoint equation

$A^T \lambda = g_x^T \leftarrow \lambda^T = g_x A^{-1}$

$g_x$通过pullback 获得。

获得：

${dg\over dp}= g_p - \lambda^T (A_p x -b_p)$

其中， $A_p, b_p$可以通过AD计算。

https://github.com/FluxML/Zygote.jl/blob/master/src/lib/array.jl 具体细节还需继续研究，还没有搞懂
第400行：

# When `A` is guaranteed to be square, definitely use the simple expression for the adjoint.
@adjoint function \(
  A::Union{
    Diagonal,
    AbstractTriangular,
    LinearAlgebra.Adjoint{<:Any, <:AbstractTriangular},
    Transpose{<:Any, <:AbstractTriangular},
  },
  B::AbstractVecOrMat,
)
  Y = A \ B
  return Y, function(Ȳ)
    B̄ = A' \ Ȳ
    return (-B̄ * Y', B̄)
  end
end

案例2: 非线性方程

$f(x,p)=0\\\\ {\partial f\over \partial x}{\partial x\over \partial p}+{\partial f \over \partial p}=0 \rightarrow {\partial x\over \partial p}=-{\partial f\over \partial x}^{-1}{\partial f\over \partial p}$ ${dg\over dp}= {\partial g \over \partial p} + {\partial g \over \partial x}{\partial x\over \partial p}=g_p-\underbrace{g_x}_{1\times M}[\underbrace{f_x^{-1}}_{M\times M}\underbrace{f_p}_{M\times P}]=g_p -\underbrace{[g_x f_x^{-1}]}_{1\times M}f_p$

计算1*M这个整体，引入adjoint equation

$f_x^T \lambda = g_x^T \leftarrow g_x f_x^{-1}=\lambda^T$

求解线性方程，using transpose of the Jacobian.

获得：

${dg\over dp}=g_p-\lambda^T f_p$

总结步骤：

Solve the nonlinear system $f(x,p)=0$ for x; “forward”
Calculate $f_x, g_p,f_p, g_x$. You’ve already calculated $f_x$ if you did a Newton method.
Solve the linear system $f_x^T \lambda=g_x$ “backward”
Explicitly calculate ${dg\over dp} = g_p -\lambda f_p$

Example: f(x,p)=2x+p, g(x,p)=x^2 +p

Step1: $2x+p =0 \space and \space so \sapce x=-p/2, g(x,p)=p^2/2+p$
Step2: $f_x=2, g_p =1, f_p=1,g_x=2x$
Step3: $2\lambda = 2x, so \lambda=x$
Step4: ${dg\over dp}=1-x$

That because for most non-linear equation, 显示解g(x,p)一般不容易获得。

Adjoint ODE

$u'=f(u,p,t)$ $G(u,p)=G(u(p))=\int_{t_0}^T g(u(t,p))dt$

To derive this adjoint, introduce the Lagrange multiplier $\lambda$ to form, the trick of adding zero:

$I(p)=G(p)- \int_{t_0}^T \lambda^* (u' -f(u,p,t))dt$

So, we can derive that:

$sensitivity: s(t) ={du(t)\over dp}\\\\ {dG\over dp}={dI\over dp}= \int_{t_0}^T (g_p +g_u s)dt - \int_{t_0}^T \lambda^* (s'-f_u s -f_p)dt$

After applying integration by parts to $\lambda^* s’$, we get that:

$\int_{t_0}^T \lambda^*(s'-f_u s -f_p)dt = \int_{t_0}^T \lambda^* s' dt - \int_{t_0}^T \lambda^*(f_u s-f_p)dt\\\\ = |\lambda^* (t)s(t)|_{t_0}^T - \int_{t_0}^T {\lambda^*} ' s dt - \int_{t_0}^T \lambda^*(f_u s-f_p)dt$

代入上式：

${dG\over dp}= \int_{t_0}^T (g_p +g_u s)dt + |\lambda^* (t)s(t)|_{t_0}^T - \int_{t_0}^T {\lambda^*} ' s dt - \int_{t_0}^T \lambda^*(f_u s-f_p)dt\\\\ = \int_{t_0}^T (g_p +\lambda^* f_p)dt + |\lambda^* (t)s(t)|_{t_0}^T - \int_{t_0}^T ({\lambda^*} ' + \lambda^* f_u -g_u)sdt$

假定：

${\lambda^*} '=-\lambda^* f_u + g_u\\\\ \lambda^* (T)=0 （step3）$

If that’s true, then:

${dG\over dp}=\int_{t_0}^T (g_p +\lambda^* f_p)dt$

引入Lagrange multiplier $\lambda$ 后，有类似之前的效果-step4。

Step1: Solve the ODE $u’ = f(u,p,t)$, this gives us u(t)
Step2: Solve the ODE ${\lambda^} ‘=-\lambda^ f_u + g_u$ in reverse, starting at T and ending at t_0, this gives us \lambda^*(t).
Step3: Solve ${dG\over dp}=\int_{t_0}^T (g_p +\lambda(t)^* f_p)dt$

Discrete cost functions

$G(u,p)= G(u(p))=\int_{t_0}^T g(u(t,p))dt\\\\ G(u,p)= \int_{t_0}^T \sum_{i=1}^N \Vert d_i -u(t_i,p)\Vert \delta(t_i -t) dt= \sum_{i=1}^N \Vert d_i -u(t_i,p)\Vert^2\\\\ g_u(t)= \sum_{i=1}^N 2(d_i - u(t,p))\delta(t_i - t)\\\\$

Solve from T to tn. You change $\lambda^$ by $g_u(t_n)$. Then you integrate $\lambda^$ to $t{n-1}$. Then change by $gu(t{n-1})$..

有关AD实现的其他阅读

考虑到反向模式自动微分的效率，我们想看看我们能将这一想法推进多远。一个没有计算图的人如何实现逆模态AD，并包含非线性求解和常微分方程之类的问题？除了拍摄方法外，还有其他方法可用于参数拟合吗？本讲座将探讨反向模式AD在何处与科学建模相交，以及机器学习在何处开始进入科学计算。

演讲12.1：分布式计算的MPI

客座讲师：Lauren E. Milechin，麻省理工学院林肯实验室和MIT Supercloud客座作家：杰里米·开普纳（Jeremy Kepner），麻省理工学院林肯实验室和MIT Supercloud

在本讲座中，我们介绍了用于分布式计算的MPI（消息传递接口）的基础知识，以及有关如何使用MPI.jl编写可在多台计算机（或“计算节点”）上有效工作的并行程序的示例。演示了在MIT Supercloud HPC上使用MPI所需的MPI编程模型和作业脚本。

演讲12.2：机器学习和高性能计算的数学

客座讲师：Jeremy Kepner，麻省理工学院林肯实验室和麻省理工学院超级云

在本讲座中，我们讨论了大数据，机器学习和高性能计算背后的数学原理。描述并演示了诸如Amdahl定律等用于描述最大并行计算效率的部分，以展示对并行计算功能的严格限制，并在大数据计算的背景下描述了这些定律，以评估该领域内分布式计算的可行性。上下文。

讲座13：GPU计算

客座讲师：Valentin Churavy，麻省理工学院朱莉娅实验室

在本讲座中，我们将更深入地探讨GPU的体系结构差异，以及这如何改变获得高效代码所需的并行计算思维方式。Valentin详细介绍了编译过程以及由于基于GPU的编程和此类硬件的直接编译中的核心权衡而导致的行为。

第14课：偏微分方程和卷积神经网络

其他读物

偏微分方程激发的深层神经网络

在本讲座中，我们将继续研究卷积神经网络与偏微分方程之间的关系，将机器学习的方法与科学计算中的方法联系起来。事实证明，它们不仅仅是相似的：两者都是对空间数据的模具计算！

第15课：连接微分方程和机器学习的更多算法

神经常微分方程和基于物理学的神经网络只是冰山一角。在本讲座中，我们将研究利用神经网络和机器学习之间的联系的其他算法。我们将使用DiffEqFlux.jl泛化为增广的神经常微分方程和通用微分方程，这现在使得刚性方程，随机性，时滞，约束方程，事件处理等都可以以神经微分方程格式进行。然后，我们将探讨通过转换为后向随机微分方程（BSDE）来求解高维偏微分方程的方法，以及通过Black-Scholes在数学金融中的应用以及通过Hamilton-Jacobi-Bellman方程的随机最优控制。然后，我们研究使用储层计算的替代训练技术，例如连续时间回波状态网络，这些技术可缓解与在僵硬和混沌动力学系统上训练神经网络相关的某些梯度问题。我们展示了一些用于自动发现符号形式的方程式的方法，例如SINDy。最后，我们研究了通过神经替代模型来加速微分方程求解的方法，并揭示了正在发生的事情的真正思想，以及了解何时可以有效地使用这些应用程序。我们展示了一些用于自动发现符号形式的方程式的方法，例如SINDy。最后，我们研究了通过神经替代模型来加速微分方程求解的方法，并揭示了正在发生的事情的真正思想，以及了解何时可以有效地使用这些应用程序。我们展示了一些用于自动发现符号形式的方程式的方法，例如SINDy。最后，我们研究了通过神经替代模型来加速微分方程求解的方法，并揭示了正在发生的事情的真正思想，以及了解何时可以有效地使用这些应用程序。

第16讲：概率编程

我们之前的所有讨论都生活在确定性世界中。不是这个。在这里，我们转向概率视图，并允许程序具有随机变量。通过蒙特卡洛采样，可以很容易地对随机程序进行前向仿真。但是，参数估计现在要涉及得多，因为在这种情况下，我们不仅需要估计值，还需要估计概率分布。事实证明，贝叶斯规则为执行此类估计提供了框架。我们看到，经典参数估计以“最简单”的分布形式作为概率的最大值落入，因此，即使是标准参数估计也可以很好地概括，并证明了使用L2损失函数和正则化（作为a的扰动）之前）。接下来，我们转向估计分布，我们发现，使用Metropolis Hastings可能会遇到一些小问题，但对于较大的问题，我们会开发Hamiltonian Monte Carlo。事实证明，哈密顿量的蒙特卡洛与ODE和可微分程序都有很强的联系：它被定义为求解由哈密顿量产生的ODE，并且需要似然的导数，这与成本函数的导数本质上是相同的！然后，我们描述一种替代方法：自动微分变异推理（ADVI），该方法再次使用可微编程的工具来估计概率程序的分布。它被定义为求解由哈密顿量产生的ODE，并且需要似然的导数，这与成本函数的导数本质上是相同的！然后，我们描述一种替代方法：自动微分变异推理（ADVI），该方法再次使用可微编程的工具来估计概率程序的分布。它被定义为求解由哈密顿量产生的ODE，并且需要似然的导数，这与成本函数的导数本质上是相同的！然后，我们描述一种替代方法：自动微分变异推理（ADVI），该方法再次使用可微编程的工具来估计概率程序的分布。

第十七讲：全球敏感性分析

我们之前对敏感性的分析都是局部的。在全球范围内举例说明模型的敏感性意味着什么？事实证明，概率编程观点为我们提供了一种可靠的方式，用于描述我们期望值如何通过描述程序输入的随机变量在较大的参数集上变化。这意味着我们可以将输出方差分解为指数，这些指数可以通过各种正交逼近来计算，然后对“变量x对均值解没有影响”给出可度量的度量。

第18课：代码分析和优化

您在本课程中如何将所有内容放在一起？让我们看一下以行形式的方法给出的PDE求解器代码。在本讲座中，我将逐步讲解代码并演示如何对其进行串行优化，并展示变量缓存和自动微分之间的相互作用。

第十九讲：不确定性编程和广义不确定性量化

不确定性编程（讲座）
不确定性编程（注释）

我们通过看另一个数学主题来结束本课程，以查看是否可以用类似的方式解决它：不确定性量化（UQ）。在某些方面可以像自动区分一样进行处理。Measurements.jl通过代表正态分布并通过程序推送这些值的数字类型，提供了一种前向传播方法，有点类似于ForwardDiff的对偶数。这具有许多优点，因为它允许不进行抽样而对不确定性进行量化，但是将数字类型转换为堆分配的值。研究了其他方法，例如严格但受范围限制的区间算法。但是在另一端，显示了一种用于ODE的非通用方法，该方法利用了微分方程解的轨迹结构，并且没有给出其他方法所看到的爆炸。该展示会使用较高级别的信息可以对UQ有所帮助，并且可能需要较少的本地方法。最后，我们将Koopman算子展示为不确定性量度的前推的伴随，并作为伴随方法，它可以针对成本函数加快不确定性的计算。